Grundfläche
Geometrie
Grundflächen gehören zu Körpern: sie sind diejenige Fläche, auf die man einen Körper normalerweise aufrecht stellen würde. Für spezielle Körper wie Kegel oder Zylinder sind die Grundflächen genau definiert. => Ganzen Artikel lesen …
Die Handfläche ist der innere Bereiche der Hand
Bei dem Wort Handfläche taucht die Frage auf, was genau damit gemeint ist. Meint man die ganze Hand vom Handgelenk bis zu den Fingerspitzen? soll man sich die Finger dann gespreizt oder zusammengelegt denken? Oder meint man mit Handfläche nur die zusammengewachsene innere Fläche ohne die Finger? In medizinischen Lexika ist die Handfläche definiert als die Fläche vom Handgelenk bis zum Anfang der Finger. Also meint man damit nur die zusammenhängende Handtellerfläche. => Ganzen Artikel lesen …
… etwa 29 % Land, 71 % Meer, mehr unter => Land-Meer-Verteilung
… ist in der Mathematik oft die => Grundfläche
bei einer Kugel spricht man nicht von einer Grundfläche.
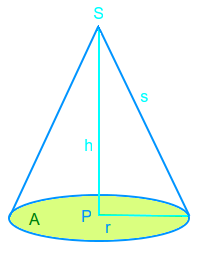Kegelgrundfläche
Definition
Die Grundfläche von einem Kegel ist ein Kreis. Um den Inhalt dieser Grundfläche zu berechnen, benutzt man die Flächenformeln für Kreis. Das ist hier kurz mit einem Zahlenbeispiel vorgestellt. => Ganzen Artikel lesen …
… Eine Ecke in der Grundfläche von einem => Vielflächner
G
Die Grundfläche einer Pyramide ist per Definition immer ein Vieleck. Pyramiden werden oft nach der Art ihrer Grundfläche benannt. => Ganzen Artikel lesen …
Anleitung
d = Durchmesser gibt es für Kreise und Kugeln. Körper wie Zylinder oder Kegel haben als Grundfläche eine Kreis. Ist der Flächeninhalt der Grundfläche bekannt, kann man daraus den Durchmesser berechnen. Eine Anleitung dazu steht unter => Kreisdurchmesser aus Kreisfläche
kommt in verschiedenen Formeln vor:
- => Pyramidenvolumen
… ist immer ein Dreieck, mehr unter => Dreieckpyramidengrundfläche
G·h oder kurz Gh, Berechnungsterm in mehreren Formeln:
- => Zylindervolumen
… mal Grundfläche G mal Höhe h, mehr unter => Kegelvolumen
G
Ein Prisma ist ein Körper. Zwei seiner Flächen sind zueinander kongruente Dreiecke. Das Dreieck das gedanklich auf dem Boden steht ist die sogenannte Grundfläche. Sie wird oft mit einem großen A oder einem großen G abgekürzt. Lies mehr unter => Prisma
… siehe unter => Dreieckpyramide
… siehe unter => Rechteckpyramide
… siehe unter => Viereckpyramide
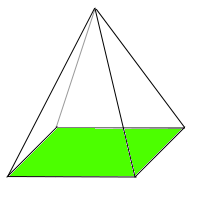Pyramidengrundfläche
Boden
Worauf die Pyramide normalerweise stehen würde: die Grundfläche ist die Seite gegenüber der Spitze. Die Grundfläche kann ein beliebiges Vieleck kann, sie darf aber nicht rund oder rundlich sein. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… mal Grundfläche G mal Höhe h, mehr unter => Pyramidenvolumen
… Grundfläche G mal Höhe h, mehr unter => Quadervolumen
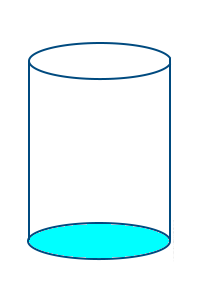Zylindergrundfläche
Definition
Die Grundfläche eines Zylinders ist seine Bodenfläche. Die übliche Abkürzung ist ein großes G. Bei einem Kreiszylinder ist die Grundfläche immer ein Kreis. Für den Flächeninhalt verwendet man dann die Formel für den Inhalt einer Kreisfläche: A = Pi mal r². Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… Grundfläche G mal Höhe h, mehr unter => Zylindervolumen
