ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
1: Graph

Bedeutungen

Funktionsgraphen, statistische Diagramme als Graphen oder reine Punktemengen in der höheren Mathematik: verschiedene Bedeutungen sind hier kurz erklärt. => Ganzen Artikel lesen …
2: Grad

Winkel | Temperaturen | Grad einer Funktion

Grad schreibt man oft als kleinen hochgestellten Kreis. Als Winkel ergeben 360° einen ganzen Kreis. Als Temperatur liegt bei 0° Celsius der Gefrierpunkt. Hier werden verschiedene Bedeutungen des Wortes Grad kurz vorgestellt. => Ganzen Artikel lesen …
3: Grän

Edelmetalle

Aus einem Lexikon des Jahres 1906: "Grän, altes Edelmetall- und Juwelengewicht. Für Gold 288 Grän = 1 preußische Mark = 1/2 preußischen Pfund oder 233,856 g. 12 Grän = 1 Karat, 24 Karat = 1 Mark. Beim Silber 18 Grän = 1 Lot, 16 Lot = 1 Mark." Siehe auch => Karat
4: Graf

Begriffsklärung

Graf oder Gräfin ist ein in Europa sehr verbreiteter Adelstitel. In der Mathematik wäre Graf einer eher ungewöhnliche Schreibweise für ein Schaudiagramm. Siehe auch unter => Graph [Mathematik]
5: Graphit

Chemisch

Als Graphit bezeichnet man elementaren Kohlenstoff mit hexagonaler Kristallstruktur. Graphit ist schwarz und ein sehr guter elektrischer Leiter. Hier stehen kurz einige Eigenschaften von Graphit aufgelistet. und ein sehr guter elektrischer Leiter. Hier stehen kurz einige Eigenschaften von Graphit aufgelistet. => Ganzen Artikel lesen …
6: Graphie

Schreibung, Beschreibung

Die Endung deutet oft auf eine schriftliche oder bildliche Darstellung hin: Lithographie, Photographie oder Kalligraphie. Im übertragenen Sinn steht es für eine naturwissenschaftliche Betrachtung, die eher den Aspekt des Daten-Erhebens und Beschreibens betont. Das wird hier kurz erläutert. => Ganzen Artikel lesen …
7: Graphen

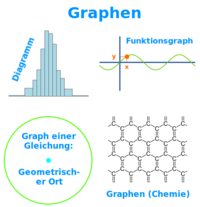
Arten

Funktionsraphen, Lösungsmengen von Gleichungen, Diagramme in der Statistik oder das Graphen (Betonung auf dem e) in der Chemie: hier stehen verschiedene Bedeutungen zu Graphen. => Ganzen Artikel lesen …
8: 0-Punkt von Graph

… zum Beispiel (11|0), mehr dazu unter => Nullpunkt von Graphen
9: 0 Punkt Graph

… so etwas wie (11|0), mehr dazu unter => Nullpunkt von Graphen
10: 2D-Koordinaten aus Graph

… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
11: 2D-Punkt graphisch

… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
12: 2D-Punktbestimmung graphisch

… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
13: 2D Koordinaten auf Graph

… für x-, y- und z-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
14: 2D Koordinaten im Graph

… für x-, y- und z-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
15: 2D Punktbestaufmung graphisch

… für x-, y- und z-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
16: 3D-Graph

z = f(x,y)

Ein 3D-Graph ist oft eine Fläche in einem xyz-Koordinatensystem. Die unabhängigen Variablen x und y bilden die Eingabe und z ist die Ausgabe. Die entsprechenden Funktionen nennt man zweidimensional, sie werden nach der Anzahl der unabhängigen Variablen benannt. Mehr unter => zweidimensionale Funktion
17: 3D-Koordinaten aus Graph

… für x-, y- und z-Werte, siehe unter => 3D-Punkt aus Koordinatensystem
18: 3D-Punkt graphisch

… für x-, y- und z-Werte, siehe unter => 3D-Punkt aus Koordinatensystem
19: 3D-Punktbestimmung graphisch

… für x-, y- und z-Werte, siehe unter => 3D-Punkt aus Koordinatensystem
20: a-t-Graph

… a meint Beschleunigung, siehe unter => Beschleunigung-Zeit-Diagramm
21: a t Graph

… a meint Beschleunigung, siehe unter => Beschleunigung-Zeit-Diagramm
22: A zwischen Graphen

… in der Integralrechnung, siehe unter => Fläche zwischen Kurven
23: A zwischen zwei Graphen

… in der Integralrechnung, siehe unter => Fläche zwischen Kurven
24: Ableiten graphisch

… f(x) gegeben, f-Strich von (x) skizzieren => Graphisch ableiten
25: Ableitung über Graph

… f(x) gegeben, f-Strich von (x) skizzieren => Graphisch ableiten
26: Ableitungen über Graphen

… f(x) gegeben, f-Strich von (x) skizzieren => Graphisch ableiten
27: Achsen- und punktsymmetrischer Graph

… das passt auf f(x)=0, also die => Nullfunktion
28: Achsensymmetrie bei Funktionsgraphen

… an der y-Achse gespiegelt, mehr unter => Achsensymmetrie von Graphen
29: Achsensymmetrie eines Graphen

… für Funktion => Achsensymmetrie von Graphen
30: Achsensymmetrie Graph

… Schmetterlingssymmetrie, mehr unter => Achsensymmetrie von Graphen
31: Achsensymmetrie Graphen

… Schmetterlingssymmetrie, mehr unter => Achsensymmetrie von Graphen
32: Achsensymmetrie von Funktionsgraphen

… an der y-Achse gespiegelt, mehr unter => Achsensymmetrie von Graphen
33: Achsensymmetrie von Graphen

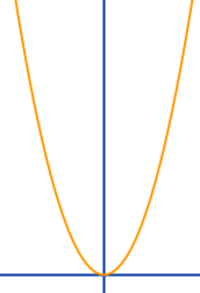
Übersicht

Achsensymmetrie heißt allgemein: der Graph einer Funktion sieht schmetterlingsartig an einer geraden Linie, der Symmetrieachse, gespiegelt aus. Im engeren Sinn ist die y-Achse (senkrechte Achse) diese Symmetrieachse. => Ganzen Artikel lesen …
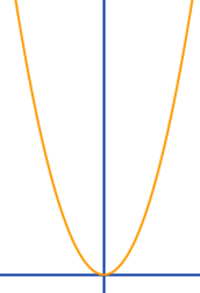34: Achsensymmetrie von Graphen überprüfen

Bedeutung | Methoden

Graphisch und rechnerisch: hier werden Methoden vorgestellt, wie man für eine gegeben Funktionsgleichung überprüft, ob der Graph achsyensymmetrisch zu y-Achse ist. => Ganzen Artikel lesen …
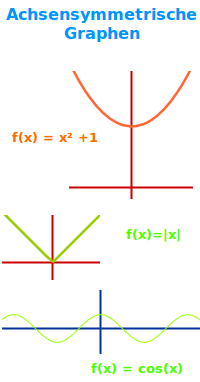35: Achsensymmetrische Graphen

Beispiele

Funktionen, deren Graph achsensymmetrisch zur y-Achse ist nennt man oft kurz achsensymmetrisch. Von der Form erscheinen sie oft schmetterlingsartig. Es gibt aber viele andere Formen. Hier stehen einige Beispiele. Eine ausführliche Erklärung steht auf der Seite zur => Achsensymmetrie von Graphen
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023