 Gleichheit
Gleichheit
Mathematik
In der Mathematik meint gleich immer nur: gleich viel, groß, lang etc. Das „gleich“ bezieht sich immer nur auf Eigenschaften, die man mit Zahlen angeben kann. Zwei Zahlen sind genau dann gleich, wenn sie auf der Zahlengeraden an derselben Stelle liegen. Für konkrete Arten, siehe unter => Gleichheiten
Arten
Zahlen, Vektoren, geometrische Formen, Beträge und einiges mehr: hier stehen konkrete Beispiele für definierte Gleichheiten in der Mathematik. => Ganzen Artikel lesen …
… in der Mathematik: nicht gleich viel, mehr unter => ungleich
Als Substantiv immer groß geschrieben
In dem Satz „Eine Differenz ist das Gleiche wie das Ergebnis einer Subtraktion“ ist das Wort „Gleiche“ ein Substantiv. Als solches wird es immer groß geschrieben. => Ganzen Artikel lesen …
… siehe unter => ungleich
… siehe unter => Potenzen mit gleicher Basis
… Begriffsklärung unter => Gleiche Basis
… ohne Vorzeichen wären es dieselben Zahlen, siehe auch => betragsgleich
… ein anderes Wort für => Kongruenz
… ≟ siehe unter => vermutete Gleichheit
… siehe unter => Potenzen mit gleichem Exponenten
… gleich große Flächen, siehe unter => flächengleich
Definition
Zwei Flächen heißen in der Geometrie gleich, wenn sie dieselbe Größe haben, also denselben Flächeninhalt. Die Form spielt dabei keine Rolle. Gleiche Formen nennt man ähnlich oder - bei gleicher Größe - auch kongruent. Hier stehen Beispiele, bei denen nur die Größe der Flächen gleich ist. => Ganzen Artikel lesen …
Geometrie
Zwei Formen - ganz gleich ob zweidimensional flach oder dreidimensional ausgedehnt - sind genau dann von der Form her gleich, wenn man die eine Form so drehen, verschieben, strecken oder spiegeln kann, dass daraus die zweite Form entsteht. Das geometrische Fachwort für diese Formengleichheit ist => Ähnlichkeit
… ≞ siehe unter => als Wert gemessen
… ≟ siehe unter => vermutete Gleichheit
… Beispiele unter => Gleichheitszeichen
… Beispiele unter => Gleichheitszeichen
Liste
≡ für identisch, ≈ für ungefähr und ≤ für kleiner oder gleich: hier steht eine Liste verschiedener Gleichheitszeichen sowie ein Tipp zur Rechtschreibung bei langen Formeln. => Ganzen Artikel lesen …
… ≙ ist das => entspricht-Zeichen
… ≙ ist das => entspricht-Zeichen
… ≙ ist das => entspricht-Zeichen
… ≟ siehe unter => vermutete Gleichheit
… etwa zum Addieren von Brüchen, siehe unter => Nenner gleichnamig machen
… ≟ siehe unter => vermutete Gleichheit
… Beispiele unter => Ungleichheitszeichen
… ≟ siehe unter => vermutete Gleichheit
 Produktgleichheit
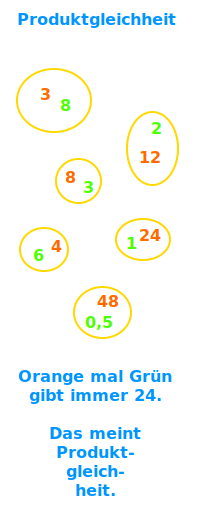
Produktgleichheit
Zwei (oder mehr) Zahlen ergeben immer dasselbe Multiplikationsergebnis
Bei einer umgekehrt proportionalen Zuordnung oder einem umgekehrt proportionalen Dreisatz gilt Produktgleichheit: wenn man zusammengehörige x- und y-Werte miteinander multipliziert, dann ergibt das Ergebnis immer dieselbe Zahl. Die immer gleiche Zahl nennt man auch den Antiproportionalitätsfaktor. => Ganzen Artikel lesen …
 Quotientengleichhheit
Quotientengleichhheit
Definition
Bei proportionalen Zuordnungen gilt Quotientengleichheit. Was das bedeutet, wie man es überprüft und was dabei die Worte „pro“, „Proportionalitätskonstante“ und „Verhältnis“ bedeuten ist hier kurz erklärt. => Ganzen Artikel lesen …
Mathematik
Oft unvollständig genanntes Kriterium: zur Überprüfung, ob zwei Größen proportional zueinander sind, wird in Schulbüchern oft die Quotientengleichheit angeführt: ein Wert einer Größe geteilt durch den dazugehörigen Wert der andreren Größe soll demnach immer das gleiche Ergebnis, nämlich die Proportionalitätskonstante ergeben. Das trifft bei Proportionalität auf alle Wertepaare außer dem Paar (0|0) zu. Die (0|0) ist per Definition zwingender Teil der Proportionalität, aber 0 geteilt durch 0 ist nicht definiert. => Ganzen Artikel lesen …
… siehe unter => Summenkonstanz
… Beispiele unter => Gleichheitszeichen
… Beispiele unter => Ungleichheitszeichen
Definition
2 ≠ 4 liest man als: zwei ist ungleich vier. Ein Gleichzeichen mit Querstrich von unten links nach oben rechts heißt ungleicht. Daneben gibt es für verschiedene Computer-Programmiersprachen noch einige andere Symbole. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… ≟ siehe unter => vermutete Gleichheit

