 Exponentialkurve
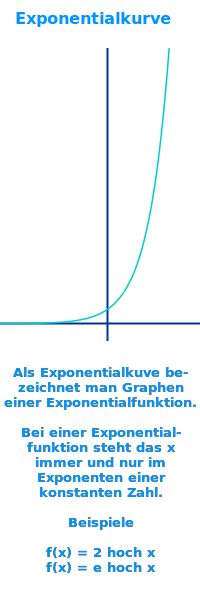
Exponentialkurve
Graph
Als Exponentialkurve bezeichnet man den Graphen einer beliebigien Exponentialfunktion (x im Exponenten). Eine Exponentialkurve wird zu einer x-Richtung hin immer flacher und zur anderen Seite him immer Steiler. Es gibt weder Extrem- noch Wendepunkte. => Ganzen Artikel lesen …
Mathematik
r·e^(i·phi) nennt man die Exponentialform einer komplexen Zahl. f(x)=4ˣ ist eine Exponentfunktion. In dem Term 2³ ist die 3 der sogenannte Exponent: hier sind verschiedene Formen mit der Bezeichnung exponential oder exponentiell kurz vorgestellt. => Ganzen Artikel lesen …
 Exponentialreihe
Exponentialreihe
… Definition: ∑ₙ=x^n/n! => Reihen
 Exponentialterm
Exponentialterm
Definition
Die Unbekannte oder Variable steht im Exponenten: als Exponentialterm bezeichnet man einen Term, bei dem eine Unbekannte oder Variable (x) im Exponenten steht. Gleichungen und Funktionen mit solchen Termen heißen entsprechend Exponentialgleichung oder Exponentialfunktion. => Ganzen Artikel lesen …
… in der Mathematik gleichbedeutend mit => exponentiell
 Einfache Exponentialkurve
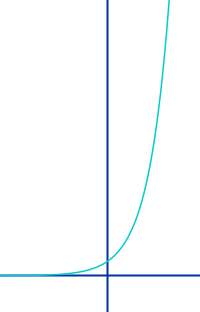
Einfache Exponentialkurve
Graph
f(x) = a^x: dies ist die einfache oder elementare Exponentialfunktion. Ihr Graph ist die einfache Exponentialkurve. Hier stehen Eigenschaftten des Graphen => Ganzen Artikel lesen …
… siehe unter => Exponentialgleichung aus zwei Punkten
… siehe unter => Exponentialgleichung aus zwei Punkten
… siehe unter => Exponentialgleichung aus zwei Punkten

