Eulerscher Polyedersatz
E+F-K = 2
Die Anzahl der Ecken plus die Anzahl der Flächen minus die Anzahl der Kanten gibt für einen Polyeder immer genau 2. Das ist der Eulersche Polyedersatz. Dieser Satz gilt für alle Körper, deren Seitenflächen Vielecke (Polyeder) sind und die keine durchgehenden Löcher (z. B. Bohrungen) haben. [1] => Ganzen Artikel lesen …
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
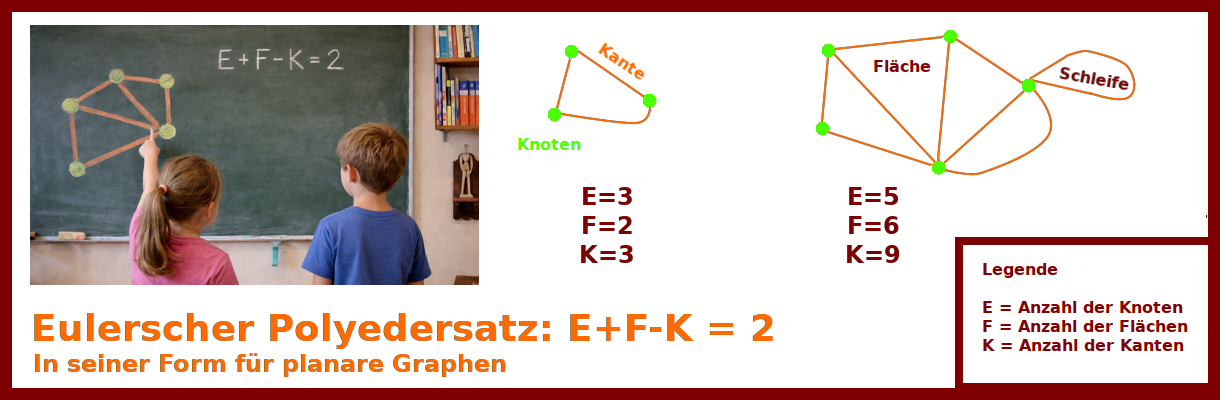Eulerscher Polygon-Versuch
Logik
Echte Mathematik ab der Klasse 1? Das geht mit einem einfachen aber tiefgründigen Beispiel aus der Graphentheorie. Je nach Interesse ist das etwas für 5 Minuten oder auch eine ganze Stunde: man zeichnet Punkte an die Tafel. Dann zeichnet man Linien, die in einem Punkt anfangen und irgendwo in einem Punkt auch wieder enden oder ins Leere gehen. Dann zählt man die Punkte, die Linien und die so erzeugten Teilflächen und macht damit eine einfache Rechnung. [4] Interessant ist das Ergebnis. => Ganzen Artikel lesen …
