Eule
… 🦉 Ein nachts aktiver Raubvogel, siehe auch => Vogelarten
Längenmaß
Länge vom Ellbogen bis zur Mittelfingerspitze: das Wort Elle bezeichnet ein Längenmaß. Da man das Wort von hinten nach vorne genauso liest wie von vorne nach hinten ist Elle auch ein sogenanntes Palindrom. Ein ähnliches Längenmaß ist die => Spann
Erle
Baum
Die Erle ist eine Baumart, die oft an ruhigen Gewässern wächst. Sie hat eine besondere biologische Fähigkeit, die sie zu einer sogenannten Pionierpflanze macht. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
In verschiedenen Kontexten:
Euler ist der Nachname verschiedener schweizer Mathematiker. Am berühmtesten ist Leonhard Euler. Nach Eulern sind verschiedene Gesetze oder Phänomene benannt. => Ganzen Artikel lesen …
Architektur
Ein senkrecht stehender Pfeiler oder eine senkrecht stehende Stütze: als Säule bezeichnet man fest gebaute auf Dauerhaftigkeit angelegte senkrechte Stützen. Sie können aus Holz, Metall oder Stein sein. An Bauwerken sind sie meistens aus Stein. Sie kann als Querschnitt rundlich sein oder auch vieleckig. Beide Fälle werden hier kurz aus Sicht der Geometrie vorgestellt. => Ganzen Artikel lesen …
… ein junger => Seehund
mit e gerundet auf 2,71828 gibt das: 0.36788
mit e gerundet auf 2,71828 gibt das: 0.135335
… etwa 2,71828, siehe für mehr => Eulersche Zahl
Eine Säule mit dreieckiger Grundfläche, ist geometrisch ein Dreieckprisma
Ein Prisma hat immer eine vieleckige Grundfläche. Die Deckfläche hat immer dieselbe Form wie die Grundfläche. Das passt auf eine Dreieckssäule. Mehr dazu unter => Dreieckprisma
mit e gerundet auf 2,71828 gibt das: 0.135335
1/e² ist rechnerisch identisch mit e hoch -2. Lies mehr unter => hoch minus zwei
… mit e gerundet auf 2,71828 gibt das: 0.36788, ist der => Kehrwert von e
… mit e gerundet auf 2,71828 gibt das: 0.135335, warum steht unter => hoch minus zwei
… für e^(iy), siehe unter => Eulersche Formel
… etwa 0,577 siehe unter => Euler-Mascheroni-Konstante
Etwa 0,577
Die Euler-Mascheroni-Konstante spielt vor allem in der Zahlentheorie und in der Analysis eine Rolle. Es ist nicht bekannt, ob die Zahl rational oder irrational ist [1]. Ihr Wert ist etwa 0,57721 56649 01532 86060 65120 90082 40243 10421 59335 93992 35988 05767 23488 48677 26777 66467 09369 47063 29174 67495. Etwas anderes ist die => Eulersche Zahl [etwa 2,71827]
… Wind der ausschließlich aufgrund von Luftdruckunterschieden entsteht, siehe auch => Wind
… etwa 2,71828, mehr unter => Eulersche Zahl
… für e^(iy), siehe unter => Eulersche Formel
… für e^(iy), siehe unter => Eulersche Formel
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
Komplexe Zahlen
e^(i*y) = cos(y) + i*sin(y) - diese eulersche Formel spielt unter anderem im Zusammenhang mit sogenannen komplexen Zahlen eine Rolle sowie in Verbindung mit Taylor-Reihen eine Rolle. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Gerade auf der drei besondere Punkte liegen
Die eulersche Gerade oder Euler-Gerade ist eine spezielle Gerade am Dreieck, eine sogenannte Dreieckstransversale, auf der eine Reihe von besonderen Dreieckpunkten liegen: => Ganzen Artikel lesen …
… für e^(iy), siehe unter => Eulersche Formel
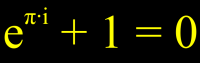Eulersche Identität
e^(i*pi) = -1
Die Eulersche Identität ist ein Spezialfall der allgemeineren Eulerschen Formel e^(iy) = cos(y) + i*sin(y). => Ganzen Artikel lesen …
Zahlenwerte
Diese Funktion gehört in das Thema Zahlentheorie. Die Funktion ist nur für natürliche Zahlen n definiert. Sie gibt zu jedem n die Anzahl zu n teilerfremder Zahlen an die nicht größer sind als n. Hier stehen einige Zahlenwerte. => Ganzen Artikel lesen …
Von n=1 bis n=500
Hier stehen die Zahlenwerte der Funktionsargumente von 1 bis 500. => Ganzen Artikel lesen …
… E+F-K=2, mehr unter => Eulerscher Polyedersatz
… e^(i*Siehe unter => Eulersche Formel
2,718281828…
2,718281828… ist der Anfang der sogenannten eulerschen Zahl, einer Konstanten ähnlich wie pi. Die Zahl ist irrational (unendlich viele Nachkommastellen, ohne Muster) und kommt in vielen mathematischen Bezügen vor. => Ganzen Artikel lesen …
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Näherungsformeln für die Eulersche Zahl unter => e annähern
