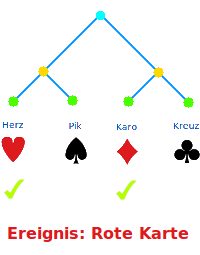
 Ereignis
Ereignis
Übersicht
Das Wort Ereignis wird sowohl in der Stochastik, also dem Rechnen mit Wahrscheinlichkeiten, wie auch in der Physik verwendet. In einem Lexikon aus dem Jahr 1793 ist ein Ereignis noch ganz allgemein eine Begebenheit. [1] Später wird noch recht vage ergänzt, dass ein Ereignis etwas ist, dass die Aufmerksamkeit auf sich zieht. [2] Eine Einengung dieser doch recht weiten Bedeutung erfuhr das Wort dann später in der Stochastik und der Physik. => Ganzen Artikel lesen …
Stochastik
Das sichere, unmögliche oder elementare Ereignis: in der Stochastik unterscheidet man verschiedene Arten, die hier kurz vorgestellt sind. => Ganzen Artikel lesen …
Mathematik
In der Stochastik und der Mathematik: das Ergebnis einer Rechnung ist meist ein Zahlenwert. Das Ergebnis eines Experimentes muss keine Zahl sein. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
ist richtig geschrieben. Eine häufige Falschschreibung ist: Zeugniss
Stochastik
Alle denkbaren Ereignisse für einen Zufallsversuches: wenn man einmal würfelt, dann sind die möglichen Ergebnisse die Zahlen eins bis sechs. Daraus kann man viele Ereignisse zusammensetzen. Ereignisse sind sozusagen Kombinationen von Ergebnissen. Alle möglichen Ereignisse zusammen gedacht ergeben den Ereignisraum. [1] Dazu steht hier ein Beispiel. => Ganzen Artikel lesen …
… in der Stochastik dasselbe wie der => Ereignisraum
- [1] "Die Menge aller Ereignisse, die sich aus der Ergebnismenge eines Zufallsexperiments bilden lassen, heißt Ereignisraum oder Ereignisfeld." In: Thomas Krickhahn: Statistik für Wirtschaftswissenschaftler Für Dummies. Wiley-VCH Verlag. 2013. ISBN: 978-3-527-70982-3. Dort im Kapitel "2.4 Ereignisse und Ereignisraum". Seite 270. Siehe auch => Ereignisraum
Beispiele
Beobachtbar, und damit auch messbar, heißt, dass man es direkt mit mindestens einem Sinnesorgan (Auge, Nase, Zungen, Tastzellen etc.) wahrnehmen kann. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
… in der Wahrscheinlichkeitsrechnung dasselbe wie => Ausgang
Raum-zeit-Koordinaten
In der der Relativitätstheorie ist ein Ereignis ein Vorfall, dem man drei Raumkoordinaten (z. B. x, y und z) sowie eine Zeitkoordinate (t) zuordnen kann. Ereignisse zwischen zueinander bewegten Koordinatensysteme können unter bestimmten Umständen ineinander transformiert (umgerechnet) werden. Mehr dazu unter => Lorentz-Transformationen
Mathematik
Irgendwas, was bei einem Zufallsexperiment herauskommen kann nennt man in der Stochastik ein Ereignis. Hier stehen Beispiele mit Karten- und Würfelspielen und auch Gegenbeispiele, was also keine Ereignisse sind. => Ganzen Artikel lesen …
… heißt in der Stochastik oft nur kurz => Ereignis
Stochastik
Ein Ereignis kann sich aus mehreren Ergebnissen (Ausgängen) zusammensetzen. Eine Definition und Beispiele stehen unter => Ereignis
… heißt in der Stochastik oft nur kurz => Ereignis
Physik
Als Ereignishorizont bezeichnet man die Entfernung vom schwarzen Loch, innerhalb derer noch nicht einmal mehr Licht den Bereich des Schwarzen Loches verlassen kann. Bei einem elektrisch neutralen und nicht rotierenden Loch hat der Ereignishorizont die Form einer Kugelfläche. Der Abstand dieses Horizontes vom Schwarzen Loch ist der => Schwarzschild-Radius
… Alle möglichen Ereignisse bei einem Zufallsexperiment => Ereignisraum
- => Ereignisraum
… heißt in der Stochastik oft nur kurz => Ereignis
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
Stochastik
Alles was nicht dazugehört: unter verschiedenen Kleepflanzen wählt man zufällig eine aus und zählt die Blätter. Man definiert als Ereignis: die Pflanze hat vier Blätter. Das Gegenereignis ist dann alles was nicht darauf passt: die Pflanze hat nicht vier Blätter. Das ist hier kurz erklärt. Als Abkürzung für das Gegenereignis eines Ereignisses A wählt man oft denselben Buchstaben mit eine darübergesetzen Querstrich (Makron), hier also Ᾱ [1]. => Ganzen Artikel lesen …
… 1-P(A), lies mehr unter => Gegenereignis
Was keine Ereignisse im Sinn der Stochastik sind
- Beim Würfeln: die Farbe des Würfels => Ganzen Artikel lesen …
Stochastik
Ein sicheres Ereignis ist eines, das mit 100 % Wahrscheinlichkeit oder einer Wahrscheinlichkeit von 1 eintritt. Jedes andere Ereignis ist dann kein sicheres Ereignis. Dazu einige Beispiele. => Ganzen Artikel lesen …
Anderes Wort für Gegenereignis
Man würfelt und betrachtet das Ereignis „Eins würfel“. Das Komplementärereignis ist dann „keine eins würfeln“: Die Wahrscheinlichkeit von einem Ereignis und seinem Gegenereignis ergibt zusammen immer Eins oder 100 %. Lies mehr unter => Gegenereignis
Stochstik
Die Anzahl der Elemente im Ergebnisraum nennt am auch die Mächtigkeit des Ergebnisraums. Man kürzt die Mächtigkeit des Ergebnisraums mit |Ω| (sprich: Betrag von Omega) ab. => Ganzen Artikel lesen …
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
Beispiele aus der Wahrscheinlichkeitsrechnung
Als sicher gilt ein Ereignis, das zu 100 % auch eintritt, es hat also die Wahrscheinlichkeit 1. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
Das was auf jeden Fall bei einem Versuch herauskäme
Ein sicheres Ereignis enthält alle möglichen Ergebnisse. Die Wahrscheinlichkeit des sicheren Ereignisses ist immer 1. => Ganzen Artikel lesen …
… heißt in der Stochastik oft nur kurz => Ereignis
… heißt in der Stochastik oft nur kurz => Ereignis
… Summe aller Ausgänge =Siehe unter => Summenregel für Ausgänge
… Summe aller Ausgänge =Siehe unter => Summenregel für Ausgänge
… Summe aller Ausgänge =Siehe unter => Summenregel für Ausgänge

