Element
Übersicht
Grundbaustein: als Element bezeichnet man den kleinsten betrachteten Baustein eines realen Gegenstandes oder auch eines Gedankengebäudes. In der Chemie bezeichnet man damit einen nicht mehr weiter zerlegbaren Reinstoff. => Ganzen Artikel lesen …
Übersicht
In der Mathematik sind Elemente Einzelteile einer Menge. In der Chemie kleinste Bestandteile von Reaktionsvorgängen und in der Historie ein Buch. Diese Bedeutungen werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Elefant
Säugetier
Der Elefant ist das zurzeit größte lebende Landtier: bis zu 3,7 Metern Schulterhöhe und 6,6 Tonnen Masse erreicht der afrikanische Elefant. Deutlich kleiner ist der afrikanische Waldelefant. In Südostastien lebt der Asiatische Elefant. Ihn erkennt man an den deutlich kleineren Ohren. Ein heute ausgestorbenener Vorfahre lebte sogar in Deutschland, das sogenannte => Deinotherium
Definition
Elementar heißt so viel wie: aus kleinsten Bausteinen gedacht, nicht mehr weiter zerlegbar, das Grundlegende. Dazu einige Beispiele. => Ganzen Artikel lesen …
… x ∉ meint => nicht Element von
Übersicht
Ein Anti-Element kann ein Element sein, das in einer mathematischen Menge fehlt (Mengenlehre) oder auch ein Element der physikalischen Antimaterie. Das ist hier kurz aufgelistet. => Ganzen Artikel lesen …
Beispiele
Ein Antielement kann ein Element sein, das in einer mathematischen Menge fehlt (Mengenlehre) oder auch ein Element der physikalischen Antimaterie. Das ist hier kurz aufgelistet. => Ganzen Artikel lesen …
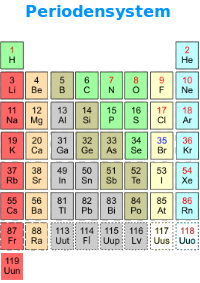Chemische Elemente
Liste
Hier steht eine Liste aller chemischen Elemente, aufsteigend angeordnet nach ihrer Ordnungszahl. Die Ordnungszahl gibt die Anzahl der Protonen im Atomkern und damit auch die Anzahl der Elektronen in einem elektrisch neutralen Atom an. => Ganzen Artikel lesen …
Chemisches Element
Definition
Ein Element im Sinne der Chemie ist ein chemisch nicht weiter zerlegbarer [1][2] Reinstoff [3], deren Eigenschaften von der Größe und Gestalt von Körpern unabhängig sind [4]: die Elemente sind die Grundstoffe der chemischen Reaktionen. Die kleinste mögliche Menge eines Elements ist das Atom. Alle Atome eines Elements haben dieselbe Anzahl an Protonen im Atomkern (die Ordnungszahl). Daher haben sie den gleichen Aufbau der Elektronenhülle und verhalten sich folglich auch chemisch gleich. Siehe auch => Ordnungszahl
Die Elemente
Geometrie
In seinem berühmtesten Werk „Die Elemente“ trug der antike griechische Philosoph und Mathematiker Euklid das Wissen der griechischen Mathematik seiner Zeit zusammen. Er zeigte darin die Konstruktion geometrischer Objekte, natürlicher Zahlen sowie bestimmter Größen und untersuchte deren Eigenschaften. Dazu benutzte er Definitionen, Postulate (nach Aristoteles Grundsätze, die akzeptiert oder abgelehnt werden können) und Axiome (nach Aristoteles allgemeine und unbezweifelbare Grundsätze). Viele Sätze der Elemente stammen offenbar nicht von Euklid selbst. Seine Hauptleistung besteht vielmehr in der Sammlung und einheitlichen Darstellung des mathematischen Wissens sowie der strengen Beweisführung, die zum Vorbild für die spätere Mathematik wurde. Lies mehr dazu im Artikel => euklidische Geometrie
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Näherungsformeln für die Eulersche Zahl unter => e annähern
Physik
Das Eigenzeitelement dτ ist ein Audruck der relativistischen Kinematik, gehört also ins Gebiet der Einsteinschen Relativitätstheorie. Der Buchstabe τ ist das kleine griechische Tau. Mit dem sogenannten Zeitdifferential dt ist es verknüpft über die Beziehung dτ = dt·√(1-v²/c²). [1] Über eine Integration erhält man aus dieser Beziehung die Eigenzeit τ, auch als T₀ bezeichnet. [2] Siehe mehr unter => Eigenzeit
… ∈ ist das => Elementzeichen
… x ∈ heißt ausgesprochen => ist Element von
… f(x)=cos(Siehe unter => Cosinusfunktion
… f(x)=e^x, siehe unter => einfache e-Funktion
… f(x) = a^x, siehe unter => einfache Exponentialfunktion
f(n)=n!
f(4) = 4! = 1·2·3·4 = 24. Für n dürfen nur natürliche Zahlen eingesetzt werden (Definitionsbereich). Lies mehr unter => Fakultätsfunktion
Definition | Beispiel
In der Mathematik: eine häufig wiederkehrerende Funktion, die als Bauteil in anderen Funktionen auftaucht. Zudem muss der Funktionswert durch eine endliche Anzahl von Rechenschritten bestimmbar sein [1]. => Ganzen Artikel lesen …
Beispiele
Elementar nennt man jede Funktion, die sich entweder nicht weiter in einfachere Funktionen zerlegen lässt oder deren Funktionswerte in einer endlichen Anzahl von Schritten berechnet werden können [1]. Dazu stehen hier Beispiele. => Ganzen Artikel lesen …
… Graph von 1/x, siehe unter => Normalhyperbel
… f(x)=1:x, mehr unter => einfache Kehrwertfunktion
… f(x)=ln(Siehe unter => einfache ln-Funktion
… mit Schwanenhalskurve, mehr unter => einfache logistische Funktion
… mit Schwanenhalskurve, mehr unter => einfache logistische Funktion
Physik-Buch
Dieses Lehrbuch bietet sehr ausführliche und lange Texte zur Einführung in Quanten- und Wellenphysik. Dazu gibt es viele Rechenbeispiele und Aufgaben mit Lösungen. Zentrale Themen sind die Quantenphysik, Atomtheorie und Relativitätstheorie. Das Buch eignet sich ab der Abiturvorbereitung. => Ganzen Artikel lesen …
… Graph von f(x)=Siehe unter => Normalparabel
… die „einfachste“ aller Sinusfunktion, Graph unter => f(x)=sin(x)
… f(x) = Wurzel x, siehe unter => einfache Wurzelfunktion
… f(x)=Siehe unter => Kubische Normalparabel
… in der Wahrscheinlichkeitsrechnung dasselbe wie => Ausgang
Elementarkompass
Versuch
Ein starker, scheibenförmiger Magnet der hochkant auf einer waagrechten und glatten Fläche steht: er wird sich immer so drehen, dass eine der flachen Seiten nach Norden und die andere nach Süden blickt. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… f(x)=Siehe unter => Kubische Normalparabel
