Matrizen
Matrix mal Vektor x = Vektor x mit neuer Länge, aber mit derselben Richtung. Die Orientierung darf eine anderere sein: „Zu einer Matrix A nennen wir v einen Eigenvektor und λ einen Eigenwert, wenn Av = λv erfüllt ist.“ [2][3] => Ganzen Artikel lesen …
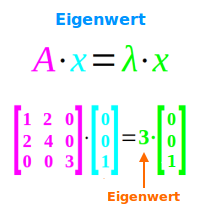Eigenwert
… Faktor λ [2] bei Längenänderung eines Vektors, mehr unter => Eigenwert und Eigenvektor
- [1] "That value of a VARIABLE to which an OPERATION defined in that variable converges (-> CONVERGENCE). Like EQUILIBRIUM, eigen values are stable points in the domain of computation and a property of the operation. E.g., x'=(x+1)/2 converges to an eigen value of 1 (-> ITERATION)." In: Klaus Krippendorf: A Dictionary of Cybernetics. Annaberg School of Economics. University of Pennsylvania. 1986. Online: https://asc-cybernetics.org/publications/Krippendorff/A_Dictionary_of_Cybernetics.pdf
Logisches UND
x=3 UND x=4 heißt: x soll gleichzeitig 3 und 4 sein. Das ist ein logischer Widerspruch. Besser ist oft das logische ODER: Möchte man beispielweise als zwei Lösungen einer pq-Formel angeben, dass einmal x=3 und einmal x=4 als Lösung gilt, dann schreibt man: x=3 ODER x=4; kurz: x=3 v x=4. Lies mehr unter => Logisches UND
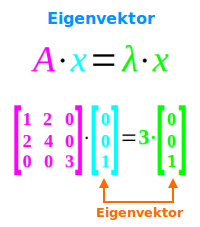Eigenvektor
Definition
A·x = λ·x: eine Matrix A wird mit einem Vektor x multipliziert. Wenn man die Matrix A durch eine reelle Zahl λ ersetzen könnte, ohne dass sich dadurch der Ergebnisvektor ändert, dann ist λ ein Eigenwert der Matrix A und x ein Eigenvektor dieser Matrix. [3] => Ganzen Artikel lesen …
Vektorrechnung
Ein Vektor, der senkrecht auf etwas steht (etwa einer Ebene) heißt Normalenvektor. Ein Vektor der genau die Länge eins hat, ist ein Einheitsvektor, auch normierter Vektor genannt. Ein Einheitsnormalenvektor ist also ein Vektor, der senkrecht auf etwas steht und genau die Länge 1 hat. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Eine Malzahl, mit der man aus alten neue Werte berechnet => Änderungsfaktoren
… das wird behandelt im Artikel zu => Ebenengleichungen
… entgegengesetzte Orientierung => Gegenvektoren
