Eigenvektor
Definition
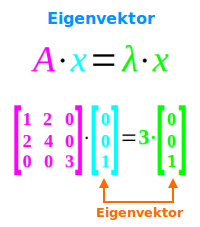
A·x = λ·x: eine Matrix A wird mit einem Vektor x multipliziert. Wenn man die Matrix A durch eine reelle Zahl λ ersetzen könnte, ohne dass sich dadurch der Ergebnisvektor ändert, dann ist λ ein Eigenwert der Matrix A und x ein Eigenvektor dieser Matrix. [3] => Ganzen Artikel lesen …
Eigenvektoren
Beispiele
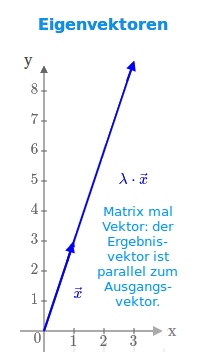
A·x = λ·x: jeder Vektor x der sich durch die Multiplikation mit einer Matrix A ledliglich in der Länge und eventuell Orientierung ändert aber noch parallel zum Ausgangsvektor x ist, heißt Eigenvektor. Hier stehen Beispiele dazu. Eine Definition steht unter => Eigenvektor
… entgegengesetzte Orientierung => Gegenvektoren
Definition
(2 0 4) ist ein Zeilenvektor: eine waagrechte Reihe von Elementen einer Matrix, also eine Matrix, die nur aus einer Zeile besten kann man auch als Zeilenvektor bezeichnen. Einen Vektor als Zeile zu schreiben, also waagrecht und mit runden Klammern, ist eine erlaubte Schreibweise [1]. Eine Matrix die nur aus einer einzelnen senkrechten Spalte besteht heißt => Spaltenvektor
Matrizen
Matrix mal Vektor x = Vektor x mit neuer Länge, aber mit derselben Richtung. Die Orientierung darf eine anderere sein: „Zu einer Matrix A nennen wir v einen Eigenvektor und λ einen Eigenwert, wenn Av = λv erfüllt ist.“ [2][3] => Ganzen Artikel lesen …
