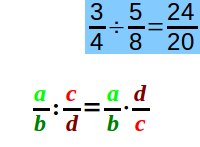Brüche dividieren
Übersicht
½:4 = ⅛ - einen Bruch zu dividieren heißt, ihn durch irgendeine andere Zahl zu teilen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
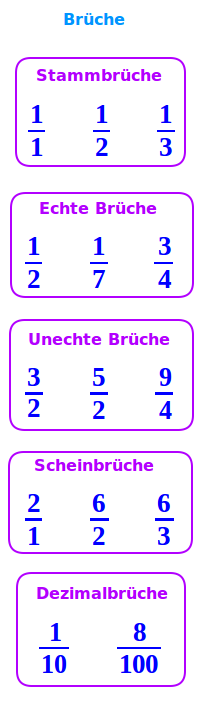Brüche
Beispiele, Arten
½, ⅘, ⅞: als Bruch bezeichnet man eine Zahl, die mit einem Bruchstrich in Bruchform geschrieben ist. Hier folgen verschiedene Arten von Brüchen (Stammbruch, echter Bruch etc.) sowie einzelne Beispiele mit Namen. => Ganzen Artikel lesen …
Rechenwege
Dividieren ist das Fremdwort für Teilen. Hier werden einige Rechenmethoden mit natürlichen Zahlen, Brüchen und Kommazahlen vorgestellt. => Ganzen Artikel lesen …
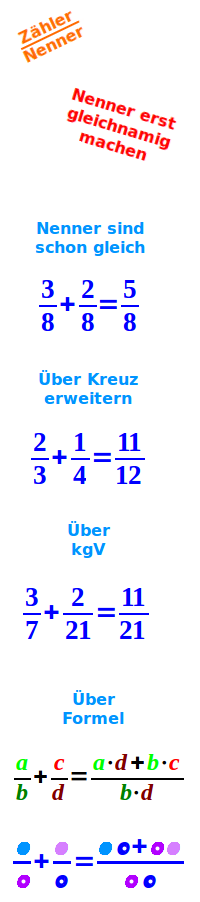Brüche addieren
Übersicht
„Brüche addieren“ kann verschiedene Aufgabentypen oder Lösungswege meinen. Hier steht eine Übersicht. In der Schulmathematik üblich ist die Addition von Brüchen über das kleinste gemeinsame Vielfache (kgV). Dieses Verfahren braucht aber viel Übung und dafür ist in der Schule nicht immer die Zeit. Ein etwas einfacheres Verfahren ist beschreiben unter => Bruch plus Bruch
… wähle unter => Brüche dividieren
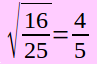Brüche radizieren
… wie 4/9 wird zu 2/3 => Wurzel aus Bruch ziehen
… siehe unter => Brüche dividieren
Anleitung
3/4 durch 1/3 ist wie 3/4 mal 3/1: Kehrwert von zweitem Bruch bilden, dann multiplizieren. Dazu hier Beispiele. => Ganzen Artikel lesen …
Anleitung
3/4 durch 5/4 gibt 3/5: rechten Bruch „umdrehen“ (Kehrbruch bilden) und dann beide Brüche malrechnen, also Zähler mal Zähler und Nenner mal Nenner. Diese Regel funktioniert immer. Sie ist hier kurz mit Zahlen vorgestellt. => Ganzen Artikel lesen …
