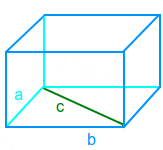
Bodendiagonale über Pythagoras
Anleitung
Länge der Bodendiagonale = Wurzel aus (a²+b²): man hat eine Kiste und soll die Länge der Strecke von einer Ecke des Bodens zur gegenüberliegenden Ecke des Bodens berechnen. Das ist hier kurz mit Hilfe des Satzes des Pythagoras erklärt. => Ganzen Artikel lesen …
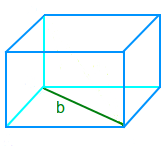Bodendiagonale
Definition
Eine Diagonale ist eine Linie zwischen zwei Ecken. Es müssen gegenüberliegende Ecken sein. Bodendiagonalen laufen unten auf dem Boden entlang. Hier steht noch etwas zur Berechnung der Bodendiagonale. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Philosoph
Pythagoras war ein antiker griechischer Mathematiker und Philosoph. Sein Name ist verbunden mit dem Satz des Pythagors a²+b²=c². Mehr zur Person unter => Pythagoras von Samos
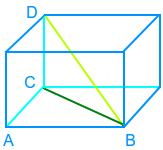Kistendiagonale über Pythagoras
Lösungsidee
Von einer rechtwinkligen Kiste, geometrisch ein Quader, soll die Länge der Raumdiagonalen berechnet werden, wenn alle Kantenlängen der Kiste bekannt sind oder leicht gemessen werden können. Über den Satz des Pythagoras berechnet man dann erst die Länge der Bodendiagonalen. Dann kann man sich mit der Bodendiagonalen ein senkrecht stehendes rechtwinkliges Dreieck denken: Die Bodendiagonale ist eine Kathete, die Kistenhöhe die andere und die Hypotenuse ist die gesucht => Kistendiagonale
Verweise zu weiteren Seiten
- => Bodendiagonale über Pythagoras
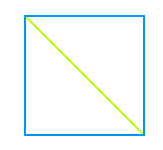Quadratdiagonale über Pythagoras
Anleitung
Diagonale = √2 mal Kantenlänge: neben dieser einfachen und genauen Formeln gibt es noch weitere Versionen. Sie beruhen alle auf dem Satz des Pythagoras und sind hier kurz vorgestellt. => Ganzen Artikel lesen …
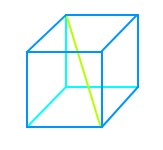Würfeldiagonale über Pythagoras
Berechnung
Die Würfeldiagonale ist die Strecke von einer Würfelstrecke, quer durch die Würfelmitte bis zur gegenüberliegenden Würfelecke. Man kann ihre Länge berechnen über die zweifache Anwendung von: c² = a² + b² => Ganzen Artikel lesen …
