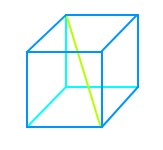
Würfeldiagonale über Pythagoras
Berechnung
© 2016
- 2025
Basiswissen
Die Würfeldiagonale ist die Strecke von einer Würfelstrecke, quer durch die Würfelmitte bis zur gegenüberliegenden Würfelecke. Man kann ihre Länge berechnen über die zweifache Anwendung von: c² = a² + b²
Formeln
- d = Wurzel aus [3·a·a] (genau)
- d = 1,73 · a (in etwa)
Legende
- d = Länge einer Würfeldiagonalen
- a = Kantenlänge des Würfels
- · = normales Malzeichen
Pythagoras
Die Länge der Würfeldiagonale kann auch mit dem Satz des Pythagoras ausgerechnet werden. Es muss dann aber das Gleiche herauskommen wie mit den Formeln oben. Eine Würfeldiagonale ist immer auch eine Raumdiagonale. Dazu berechnet man erst die Länge der Bodendiagonale des Würfels über Pythagoras. Die Bodendiagonale bildet dann mit einer senkrechten Würfelkante und der Würfeldiagonalen ein senkrecht stehendes rechtwinkliges Dreieck, welches man wiederum über Pythagoras berechnen kann.