Definition
Als Vektorraum bezeichnet man eine Gesamtheit von Vektoren, die miteinander addiert, subtrahiert und die auch mit Zahlen multipliziert werden können. Als Basis eines solchen Vektorraums kann man jede beliebige Teilmenge defieren, also immer irgendwelche Vektoren, die man so als Linearkombination verbinden kann, dass man damit jeden anderen Vektor des gesamten Vektorraums darstellen kann. Das ist hier kurz mit einem Beispiel vorgestellt. => Ganzen Artikel lesen …
 Basis
Basis
Mathematik
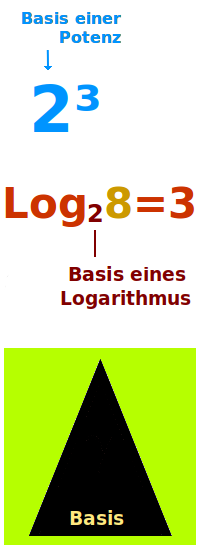
Als Basis bezeichnet man ganz allgemein Dinge, die unten sind. Bei der Potenz 2³ ist die Zahl 2 entsprechend die Basis, nämlich die Zahl, die unten steht. Von einer Basis spricht man zum Beispiel auch bei Logarithmen, Dreiecken, Trapezen, Geodreiecken, Vektoren oder ganzen Weltbildern. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
… siehe unter => Basis (Vektorraum)
Definition
U ist ein Untervektorraum vom Vektorraum V, wenn a) U das neutrale Element der Addition von V enthält und b) zwei Elemente von U addiert immer nur wieder ein Element von U ergeben und c) ein Element von U skalar multipliziert mit einem Element von K wieder ein Element von U ergibt. Siehe auch => Vektorraum
Notizen, noch kein Artikel
Ein Vektorraum im engeren Sinn besteht aus einer Menge von Vektoren und einer Zahlenmenge (z. B. die reellen Zahlen) für die gemeinsam bestimmte Rechenregeln formuliert sind. Die schulmathematische Vektorrechnung arbeitet mit einem Vektorraum. In der höheren Mathematik wird der Begriff aber stark erweitert. => Ganzen Artikel lesen …

