 Basis
Basis
Mathematik
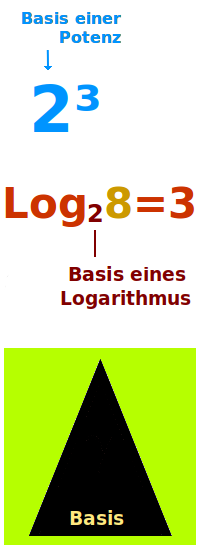
Als Basis bezeichnet man ganz allgemein Dinge, die unten sind. Bei der Potenz 2³ ist die Zahl 2 entsprechend die Basis, nämlich die Zahl, die unten steht. Von einer Basis spricht man zum Beispiel auch bei Logarithmen, Dreiecken, Trapezen, Geodreiecken, Vektoren oder ganzen Weltbildern. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
… Name einiger einfacher Programmiersprachen, z. B. der Dialekt => Basic256
Als griechische Silbe: König
Basilosaurus, Basilika oder auch Basilikum: basil hat oft die Bedeutung von König. Hier stehen einige (wenige) Beispiele. => Ganzen Artikel lesen …
Astronomie | Architektur
=> Ganzen Artikel lesen …
… ph-Wert über 7,0, siehe auch => ph-Werte
… so etwas wie 2²+2³ => Potenzen mit gleicher Basis addieren
… 2³ = e hoch was? siehe unter => Potenzbasis umwandeln
… 2³ = e hoch was? siehe unter => Potenzbasis umwandeln
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
Definition
Als Vektorraum bezeichnet man eine Gesamtheit von Vektoren, die miteinander addiert, subtrahiert und die auch mit Zahlen multipliziert werden können. Als Basis eines solchen Vektorraums kann man jede beliebige Teilmenge defieren, also immer irgendwelche Vektoren, die man so als Linearkombination verbinden kann, dass man damit jeden anderen Vektor des gesamten Vektorraums darstellen kann. Das ist hier kurz mit einem Beispiel vorgestellt. => Ganzen Artikel lesen …
 Basis einer Potenz
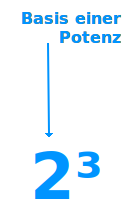
Basis einer Potenz
Definition
Bei 2³ ist die 2 die Basis: das ist immer die die Zahl unten in einer Potenz. Hier wird die Bedeutung der Basis kurz erklärt. => Ganzen Artikel lesen …
 Basis eines Logarithmus
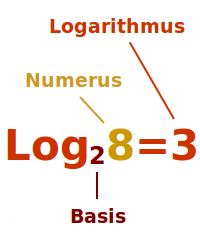
Basis eines Logarithmus
Die Zahl, die gedanklich hochgerechnet wird
Das Logarithmieren ist das Potenzieren rückwärts gedacht. Der Logarithmus von 100 zur Basis 10 ist 2. Das meint: 10 hoch 2 gibt 100. Die Basis von einem Logarithmus ist immer die gleiche Zahl, die auch in der Potenzschreibweise die Basis wären. In dem Beispiel oben wäre also die 10 die Basis. Siehe auch => Logarithmenbasen [Beispiele]
… längere der parallelen Seiten, mehr unter => Trapezbasis
… siehe unter => Potenzen mit gleicher Basis
… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent
… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent
… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent
… Begriffsklärung unter => Gleiche Basis
… siehe unter => Potenzen mit gleicher Basis
… z. B. (-2)³, siehe unter => Negative Zahlen potenzieren
… Beispiele unter => Logarithmenbasis
… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent
… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent
… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
… längere der parallelen Seiten, mehr unter => Trapezbasis
… 2³ = e hoch was? siehe unter => Potenzbasis umwandeln
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
… 2³ = e hoch was? siehe unter => Potenzbasis umwandeln
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
… z. B.: 2³ ⭢ e-hoch-irgendwas => Potenzbasis umwandeln
… wie Meter, Kilogramm etc., siehe => SI-Basiseinheiten

