 Anzahl von Nullstellen
Anzahl von Nullstellen
Hängt ab vom Funktionstyp
Wie viele Nullstellen der Graph einer Funktion haben kann hängt vom Funktionstyp ab. Hier werden häufig behandelte Fälle kurz vorgestellt. => Ganzen Artikel lesen …
 Anzahl
Anzahl
Die zählbare Menge
Das was beim reinen Zählen herauskommt ist die Anzahl. Die Anzahl der r's in dem Wort Rollreibung ist genau 2. Die Anzahl der o's (groß und klein zusammengezählt) in dem Wort Ottomotor ist genau 4. Eine Anzahl ist immer eine ganze Zahl und nie negativ. In der Statstik nennt man die Anzahl oft auch absolute Häufigkeit. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
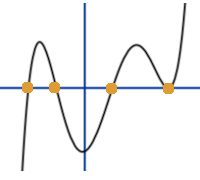
![Graph der Funktion f(x) = [(x + 2)·(x + 1)·(x 1)·(x 3)²] / 8](bilder/nullstellen.png) Nullstellen
Nullstellen
Beispiele
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen. => Ganzen Artikel lesen …
… siehe unter => Nullstellen von Geraden
… Schnittpunkt mit x-Achse, siehe => Nullstellen von Parabeln
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
ABC steht für die sogenannte ABC-Formel zum Lösen quadratischer Gleichungen. Die Funktion f(x) = Ax² + Bx + C hat die Nullstellen [-B ± Wurzel aus (B² - 4A·C)] durch [2A]
… Schnittpunkt mit x-Achse, siehe => Nullstellen von Parabeln
… siehe unter => Anzahl von Nullstellen

