f(x) = ax²+bx+c in a·(x-d)²+e
Die allgemeine Form [1] bezieht sich hier auf quadratische Funktionen bzw. Gleichungen. Es gibt verschiedene Verfahren, sie in die Scheitelpunktform umzuwandeln. => Ganzen Artikel lesen …
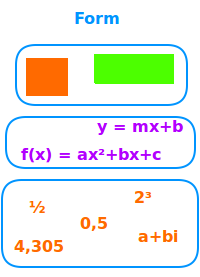Form
Mathematik
Die Gestalt einer Figur, eine Gleichung oder auch Zahlen: in der Mathematik bezieht sich das Wort Form auf verschiedene Dinge. Das ist hier einzeln vorgestellt. => Ganzen Artikel lesen …
Übersicht
In als das Element Indium oder die Umwandlung einer Zahl oder Einheit in eine andere Art: das Wort in hat verschiedene Bedeutungen. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
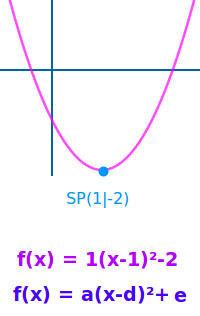Scheitelpunktform
f(x) = a·(x-d)² + e
Von quadratische Funktionen und Parabeln: aus der Scheitelpunktform y oder f(x) = a·(x²-d)²+e kann man leicht den Scheitelpunkt, die Öffnung und den y-Achsenabschnitt ablesen einer Parabel in einem xy-Koordinatensystem ablesen. Umgekehrt kann man sie leicht aufstellen, wenn man von einer Parabel den Scheitelpunkt SP und irgendeinen weiteren Punkt kennt. Das ist im Folgenden beschrieben. => Ganzen Artikel lesen …
… Rechenbeispiel unter => Scheitelpunktform in Allgemeine Form
… ist a(x-d)²+e, heißt einfach nur => Scheitelpunktform
Anleitung
Eine quadratische Funktion in allgemeiner Form f(x)=4x²-24x+32 wird umgeformt in die Scheitelpunktform: f(x)=4·(x-3)²-4. Wie das mit Hilfe der quadratischen Ergänzung (QE) geht wird hier in kleinen Schritten erklärt. => Ganzen Artikel lesen …
Anleitung
Eine Funktion der Form f(x) = ax²+bx+c kann man immer umwandeln in die Scheitelpunktform f(x) = a·(x-d)²+e. In der Schulmathematik wird das oft mit Hilfe der quadratischen Ergänzung (QE) gemacht. Hier ist eine Alternative dazu, die für praktische Zwecke dasselbe Ergebnis liefert. => Ganzen Artikel lesen …
… Rechenbeispiel unter => Allgemeine Form in Scheitelpunktform
