ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
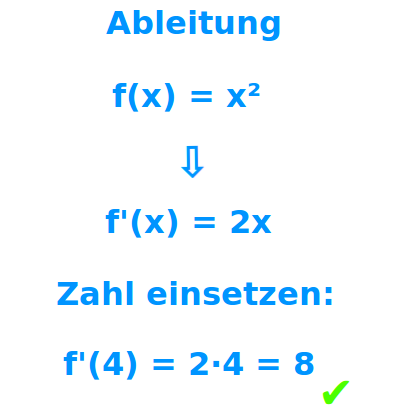
1: Ableitung

f'(x)

Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
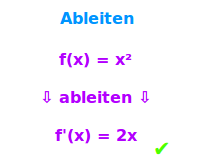
2: Ableiten

Verfahren

Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
3: Ableitungen

Arten | Beispiele

Als Ableitung f'(x) bezeichnet man im erweiterten Sinn die Ableitungsfunktion zu einer gegebenen Funktion f(x). Man unterscheidet eine erste, zweite, dritte Ableitung etc. Ableitungen werden auch nach der Art der Ausgangsfunktion f(x) unterteilt. Auf dieser Seite stehen einige Beispiele. => Ganzen Artikel lesen …
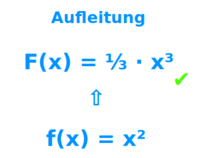
4: Aufleitung

Stammfunktion

Eine Aufleitung F(x) von einer Funktion f(x) ist dasselbe wie eine Stammfunktion von f(x). Das Wort wird häufig benutzt, um den Zusammenhang mit der entegegengesetzen Operation der Ableitung zu verdeutlichen. Lies unter => Stammfunktion
5: Leitung

… für Flüssigkeiten, Gase, Elektrizität, siehe auch => elektrischer Leiter
6: 3. Ableitung

… also f''', siehe unter => dritte Ableitung
7: 0 bei erster Ableitung

… Bedeutungen unter => erste Ableitung gleich null
8: 0 bei zweiter Ableitung

… was das bedeutet unter => zweite Ableitung gleich null
9: 0 für erste Ableitung

… Bedeutungen unter => erste Ableitung gleich null
10: 0 für zweite Ableitung

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
11: 0te Ableitung

… die noch gar nicht abgeleitete Funktion, mehr unter => eigentliche Funktion
12: 1. Ableitung

… gibt die Steigung einer Funktion, ausführlich erklärt unter => Erste Ableitung
13: 2. Ableitung

… gibt die Krümmung, alles Weitere unter => Zweite Ableitung
14: 2. Ableitung 0

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
15: 2. Ableitung gibt null

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
16: 2. Ableitung gleich 0

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
17: 2. Ableitung gleich null

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
18: 2. Ableitung null

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
19: 2te Ableitung gleich 0

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
20: 2te Ableitung gleich null

… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
21: 3te Ableitung

… also f'Siehe unter => dritte Ableitung
22: Doppelableitung

… f''(x) oder partielle Ableitung, siehe unter => Doppelte Ableitung
23: Ableitung an einem Punkt

… steht unter => Steigung in einem Punkt
24: Ableitung der e-Funktion

… über Kettenregeln, mit Beispielen => e-Funktion ableiten
25: Ableitung der einfachen a hoch x Funktion

a^x abgeleitet gibt a^x·ln(a)
26: Ableitung der einfachen e-Funktion

e^x abgeleitet gibt wieder e^x
27: Ableitung der einfachen Exponentialfunktion

… a^x abgeleitet gibt a^x·ln(a), allgemeiner unter => Exponentialfunktion ableiten
28: Ableitung der einfachen Ln-Funktion

… ln(x) abgeleitet gibt: 1/x siehe auch => Logarithmusfunktion ableiten
29: Ableitung der Einsfunktion

… also von f(x)=0, steht unter => Einsfunktion ableiten
30: Ableitung der natürlichen Logarithmusfunktion

… ln(x) abgeleitet gibt: 1/x => Logarithmusfunktion ableiten
31: Ableitung der Nullfunktion

… also von f(x)=0, steht unter => Nullfunktion ableiten
32: Ableitung Differenz

… jedes Glied einzeln ableiten, mehr unter => Ableiten über Summenregel
33: Ableitung einer konstanten Funktion

f(x)=4 abgeleitet gibt f'(x)=0

Kurz erklärt: Eine konstante Funktion hat immer die Form: f(x) = Zahl. Die Ableitung ist f'(x) ist immer 0. Mehr dazu unter => Konstante Funktion ableiten
34: Ableitung einer kubischen Funktion

… hoch-drei-Funktion => kubische Funktion ableiten
35: Ableitung einer linearen Funktion

4x+2 abgeleitet gibt 4

Kurz erklärt: Eine lineare Funktion kann man immer umformen in f(x)=m·x+b. Die Ableitung ist dann allgemein: f'(x)=m. Beispiel: f(x)=4x+2 abgeleitet gibt f'(x)=4. Mehr dazu unter => Lineare Funktion ableiten
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023