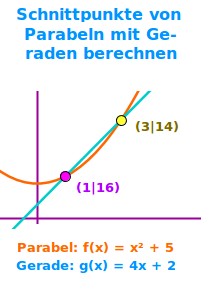
Schnittpunkte von Parabeln mit Geraden berechnen

11 Standardaufgaben für den Einstieg

Bestimme alle Schnittpunkte der Geraden g(x) mit der Parabel p(x). Es kann keinen, genau einen oder auch zwei Schnittpunkte geben.

a)

Bildbeschreibung und Urheberrecht — Die orangene Parabel f(x) = x²+5 und die blaue Gerade g(x) = 4x + 2 haben hier genau zwei Schnittpunkte.☛

g(x) = -3x + 1
p(x) = x² + 2x - 5

b)

g(x) = 1/2 x - 2/3
p(x) = x² + 1/3 x - 5/6

c)

g(x) = 4
p(x) = x² - 6x + 13

d)

g(x) = 3x + 17
p(x) = 4x² - 7x + 11

e)

g(x) = -20x - 4
p(x) = 3x² - 2x + 11

f)

g(x) = - 5x + 2
p(x) = 84x² + 7x + 9

g)

g(x) = 1/4 x
p(x) = 12x² - 13x

h)

g(x) = 1/12 x + 3/16
p(x) = x² - 1/6 x + 5/16

i)

g(x) = -3/32 x + 9/32
p(x) = x² + 1/32 x - 5/16

j)

g(x) = 4
p(x) = x² - 4x + 2/3

k)

g(x) = 3x - 6
p(x) = x² - 2x + 4

Lösungen

a)

S1 ( 1 | - 2 )
S2 ( - 6 | 19 )

b)

S1 ( 1/2 | -5/12 )
S2 ( - 1/3 | - 5/6 )

c)

S1 ( 3 | 4 )

d)

S1 ( 3 | 26 )
S2 ( -1/2 | 31/2 )

e)

S1 ( - 1 | 16 )
S2 ( - 5 | 96 )

f)

Es gibt keine Schnittpunkte

g)

S1 ( 0 | 0 )
S2 ( 53/48 | 53/192 )

h)

S1 ( 1/2 | - 7/48 )
S2 ( - 1/4 | - 5/24 )

i)

S1 ( - 1 | 21/32 )
S2 ( 7/8 | 123/256 )

j)

S1 ( 4 | 2/3 )

k)

Es gibt keine Schnittpunkte