Schnittpunkte von Parabeln mit Geraden berechnen
Anleitung
Basiswissen
Eine Parabel und eine Gerade können keinen, genau einen oder genau zwei Schnittpunkte haben. Hier ist ein Verfahren beschrieben, das immer alle vorhandenen Schnittpunkte bestimmt.
Voraussetzung
◦ Die Gleichung einer Geraden ist eine lineare Funktion.
◦ Die Gleichung einer Parabel ist eine quadratische Funktion.
Beispiel
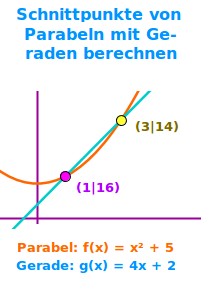
◦ Beispiel Parabel: f(x) = x² + 5
◦ Beispiel Gerade: g(x) = 4x + 2
Schritt 1: gleichsetzen
◦ Man setzt die rechten Seiten, also die Funktionsterme, gleich:
◦ Gleichsetzen: 4x + 2 = x² + 5
Schritt 2: in Normalform umwandeln
◦ Die Normalform ist: 0 = x²+px+q
◦ Mit der Normalform kann die pq-Formel benutzt werden.
◦ 4x + 2 = x² + 5 | -4x
◦ 2 = x² + 5 - 4x | -2
◦ 0 = x² - 4x + 3
Schritt 3: pq-Formel anwenden
◦ Anleitung unter => quadratische Gleichungen über pq-Formel
◦ Die Lösungen der Gleichung sind: x1=1 und x2=3
◦ Das sind die x-Werte der Schnittpunkte.
Schritt 4: y-Werte bestimmen
◦ Damit die y-Werte der Schnittpunkte berechnen:
◦ Dazu x1 und x2 in die Geradengleichung einsetzen:
◦ x1 = 1 gibt y1 = 14
◦ x2 = 3 gibt y2 = 6
Schritt 5: Punkte notieren
◦ Ein x- und ein y-Wert zusammen ergeben einen Punkt.
◦ Hier hat man zwei Schnittpunkte:
◦ Schnittpunkt 1: P1 (1|16)
◦ Schnittpunkt 2: P2 (3|14)
Sonderfälle
◦ Liefert die pq-Formel nur eine Lösung, gibt es nur einen Schnittpunkt.
◦ Liefert die pq-Formel keine Lösung, gibt es keine Schnittpunkte.
