Extremwertaufgaben über Analysis
7 Aufgaben mit Lösungen
a) Weidefläche
- An einem geraden Fluss soll eine rechteckige Weidefläche eingezäunt werden.
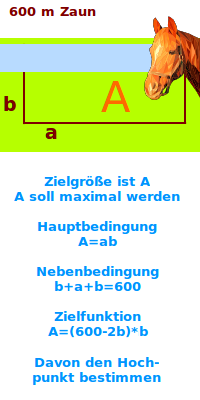
- Die drei anderen Seiten benötigen allerdings Zaun.
- Insgesamt hat man 120 Meter Zaunlänge zur Verfügung.
- Wie lang und breit wird die Weidefläche, ...
- wenn ihre Fläche maximal sein soll?
b) Vorratskammer
- An eine Hauswand soll eine quaderförmige (Rechteckkiste) Vorratskammer gebaut werden.
- Die Grundfläche der Vorratskammer soll quadratisch sein.
- Insgesamt stehen dafür 48 m² Holzplatten zur Verfügung.
- Was ist die Höhe für das maximale Volumen?
c) Produkt I
- Die Zahl 100 soll in zwei positive Summanden zerlegt werden.
- Das Produkt der Summanden soll möglichst groß werden.
- Wie lauten die Summanden?
d) ProduktII
- Die Zahl 80 soll in zwei Summanden zerlegt werden.
- Keiner der Summanden darf dabei negativ sein.
- Das Produkt der Summanden soll möglichst klein werden.
- Wie lauten die Summanden?
e) Kurvenfläche
- Man hat den Graphen der Funktion f(x)=4-0,5x.
- Der Definitionsbereich geht von x=0 bis x=8.
- Auf dem Graphen selbst sei frei beweglich der Punkt P.
- Für P erlaubt sind nur x-Werte von 0 bis 8.
- Von P ausgehend soll man sich eine waagrechte und ...
- eine senkrechte Linie vorstellen. Diese zwei Linien ...
- bilden mit der x- und y-Achse ein Rechteck.
- Wo muss P auf der Geraden liegen, dass der ...
- Flächeninhalt des Rechtecks maximal wird?
f) Rechteckfläche
- Man hat Material für 120 Meter Zaun.
- Damit soll eine rechteckige Weidefläche umzäunt werden.
- Der Zaun soll alle vier Seiten komplett umschließen.
- Bei welcher Länge und Breite des Rechtecks kann welche maximale Fläche umzäunt werden?
g) Weidezaun mit Tor
- Man hat Material für 150 Meter Zaun.
- Damit soll eine rechteckige Weidefläche eingezäunt werden.
- Eine der vier Seiten ist ein Fluss. Dort ist kein Zaun nötig.
- An der Seite gegenüber des Flusses soll ein Tor in den Zaun gebaut werden.
- Das Tor soll genau halb so breit sein wie diese Seite.
- Wie breit und wie lang ist die Weidefläche, wenn ...
- der Flächeninhalt maximal werden soll?
Lösungen
Lösungen
a) Länge 60 m, Breite 30 m
b) Würfel mit Kantenlänge von etwa 40,8 cm
c) noch keine Lösung
d) 80 und 0
e) P(4|2)
f) Das optimale Rechteck wäre ein Quadrat mit 30 m Kantenlänge. Die Fäche wäre dann 900 m².
