y-Achsenabschnitt von Parabeln berechnen
Anleitung
© 2016
- 2025
Basiswissen
Für x die Zahl 0 in den Funktionsterm einsetzen und dann f(0) ausrechnen. Das Ergebnis ist der y-Achsenabschnitt. Das ist hier weiter erklärt.
Parabel
- Parabel meint hier den Graphen einer quadratischen Funktion.
- (In der Geometrie kann Parabel etwas anderes meinen.)
y-Achsenabschnitt
- Die y-Achse ist die senkrechte Achse von unten nach oben.
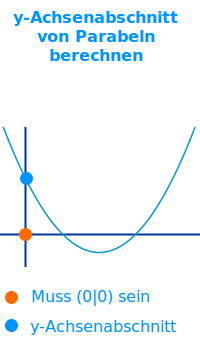
- Für das folgende Verfahren muss die y-Achse durch den Punkt (0|0) gehen.
- Wo die Parabel durch die y-Achse geht ist der y-Achsenabschnitt.
- Jede Parabel hat immer genau einen y-Achsenabschnitt.
- Der x-Wert vom y-Achsenabschnitt ist immer 0.
- Der y-Wert ist gesucht.
Berechnung
- Man setzt für x immer die Zahl 0 ein.
- Beispiel: y = x² + 8x + 10
- 0 einsetzen: y = 0² + 8·0 + 10
- Gibt: y = 10
Antwort
- 1. Möglichkeit: der y-Achsenabschnitt liegt bei y=10.
- 1. Möglichkeit: der y-Achsenabschnitt ist bei (0|10).
- 2. Möglichkeit: der y-Achsenabschnitt Sy (0|10).
Tipps
- 3x² meint dasselbe wie 3 mal x².
- 3·(-2x²) gibt -6x²
- Klammern immer erst auflösen
- Erst alles im Term zuammenfassen
- Eventuell nach dem Einsetzen nach y umstellen.
- Der y-Achsenabschnitt kann auch eine Minuszahl sein.
- Statt y steht auch oft f(x). Das meint hier dasselbe.