Basiswissen

Der Vektor (1|1|1) plus den Vektor (2|2|7) gibt den Vektor (3|3|8): rechnerisch ergibt sich die Summe aus der zeilenweisen Addition aller Koordinaten. Graphisch bildet man aus den Vektoren eine Kette. Die Summe der Vektoren ist dann der kürzeste Vektor vom Anfang der Kette bis zu ihrem Ende. Beides wird hier kurz erklärt.

Bildbeschreibung und Urheberrecht — Blauer Vektor plus lila Vektor gleich grüner Vektor☛

Vektore geometrisch addieren

Als Vektorkette

Man hat zwei oder mehr Vektoren gegeben.

Jeder Vektor hat ein hinteres Ende (ohne Spitze), den Anfangspunkt.^[1]

Und jeder Vektor hat ein vorderes Ende (mit Spitze), den Endpunkt^[1]

Man fügt alle Vektoren dominoartig so aneinander dass ...

auf eine Spitze immer ein hinteres Ende folgt. Das Ergebnis ist eine Vektorkette.

Man zieht dann einen geraden Strich vom Anfang der Kette (Punkt ohne Spitze) ...

bis zur letzten Spitze der Vektorkette. Dort erhält der gezeichnet Strich seine Spitze.

Dieser gezeichnete Strich mit der Spitze ist die Summe aller Vektoren der Kette.

In der Physik nennt man die Vektorsumme oder auch die Resultierende ↗

Siehe auch Vektoraddition ↗

Als Kräfteparallelogramm

Insbesondere in der Physik addiert man zwei Vektoren oft auch über ein sogenanntes Kräfteparallelogramm. Die Methode wurde bereits von Isaac Newton beschrieben.^[2] Man zeichnet die zwei gegebenen Vektoren so, dass ihre Anfangspunkte (ohne Pfeilspitze) in einem Punkt liegen. Dazu darf man die Vektoren beide immer beliebig zu sich selbst parallel verschieben. Dann ergänzt man die zwei Vektoren zu einem Parallelogramm.^[3] Die Diagonale, die im gemeinsamen Anfangspunkt der zwei Vektoren liegt, hin zur gegenüberliegenden Ecke ist dann der gesuchte Summenvektor. Siehe mehr unter Kräfteparallelogramm ↗

Vektoren rechnerisch addieren

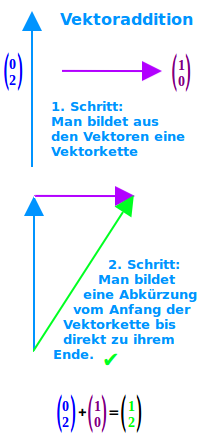
Vektoren bestehen aus einzelnen Zahlen, den sogenannten Vektorkoordinaten. Um zwei oder mehr Vektoren rechnerisch zu addieren, addiert man alle entsprechenden Vektoren. Beispiel: die Vektoren (0|2) und (1|0) ergeben addiert die Summe (1|2).

Beispiele

(1|0|0)+(0|2|0)+(0|0|3) = (1|2|3)

(2|0|0)+(0|2|0)+(0|0|2) = (2|2|2)

(1|1|1)+(2|2|2)+(3|3|3) = (6|6|6)

Fußnoten

[1] Eine moderne Fassung der Addition von Vektoren: "Zwei Vektoren a und b werdne nach der folgenden Vorschrift geometrisch addiert: 1) Der Vektor b wird parallel zu sich selbst verschoben, bis sein Anfangspunkt in den Endpunkt des Vektors a fällt. 2) Der vom Anfangspunkt des Vektors a zum Endpunkt des verschobenen Vektors b gerichtete Vektor ist der Summenvektor s=a+b." Die Namen s, a und b der Vektoren tragen im Original jeweils einen Pfeil über sich. In: Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Dort das Kapitel "1.4.1 Addition von Vektoren". Seite 49.

[2] Wie man zwei Vektoren addiert und dass dabei Resultierende zweier Vektoren die Diagonale eines Parallelogramms ergibt, hat bereits der englische Naturphilosoph Isaac Newton (1642 bis 1727) im Jahr 1687 beschrieben: "A body by two forces conjoined will describe the diagonal of a parallelogram, in the same time that it would describe the sides, by those forces apart." Und: "And hence is explained the composition of any one direct force AD, out of any two oblique forces AC and CD ; and, on the contrary, the resolution of any one direct force AD into two blique forces AC and CD: which composition and resolution are abundantly confirmed from, mechanics." In: THE MATHEMATICAL PRINCIPLES OF NATURAL PHILOSOPHY (1687). BY SIR ISAAC NEWTON. TRANSLATED INTO ENGLISH BY ANDREW MOTTE (1846). Online: https://archive.org/details/newtonspmathema00newtrich

[3] Jedes Viereck, bei dem gegenüberliegende Seiten immer zueinander parallel sind, nennt man ein Parallelogramm ↗