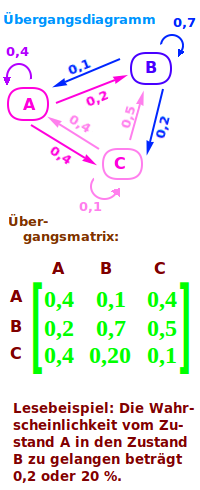
Übergangsmatrix aus Übergangsdiagramm
Schritt-für-Schritt Anleitung
© 2016
- 2025
Basiswissen
Es ist das Übergangsdiagramm eines stochastischen Prozesses gegeben. In der Schulmathemati werden nur sogenannte Markow-Ketten behandelt: Mit einem Übergangsdiagramm kann man aus einem gegebenen Gesamtzustand die Wahrscheinlichkeit für den Folgezustand berechnen.
Übergangsdiagramm
- Das Diagramm besteht aus Ovalen, Kreisen oder Rechtecken.
- Das sind die Zustände, ihre Anzahl sei n.
- Von jedem dieser Elemente geht ein Pfeil zu jedem anderen Element.
- Von jedem Element geht ein Pfeil zu sich selbst.
- An jedem Pfeil steht eine Zahl zwischen 0 und 1.
- Diese Zahlen können auch %-Angaben sein.
- Alle Pfeile, die von einem bestimmten Element ausgehen,
- müssen in Summe immer die Zahl 1 ergeben.
- Fehlt ein Pfeil, kann man ihn nachtragen.
- Im ordnet man die Zahl 0 oder 0 % zu.
Tabelle anlegen
- Zeichne eine Tabelle mit n+1 Spalten (von oben nach unten).
- Die Tabelle hat auch n+1 Zeilen (von links nach rechts.)
- Schreibe in die oberste Zeile von links nach rechts die Zustände.
- Schreibe in die linke Spalte von oben nach unten die Zustände.
Tabelle ausfüllen
- Jeder Pfeil aus dem Diagramm meint: Vom Zustand X zum Zustand Y.
- Das von meint die Überschriften der Spalten (stehen alle oben).
- Das zu meint die Überschrift der Zeilen (stehen alle links).
- Trage die entsprechenden Wahrscheinlichkeiten so ein.
Kontrolle
- Bilde für jede einzelne Spalte die Summe (Addition).
- Jede Spalte für sich muss die Summe 1 oder 100 % haben.
- Falls das nicht so ist, ist irgendwo ein Fehler vorhanden.