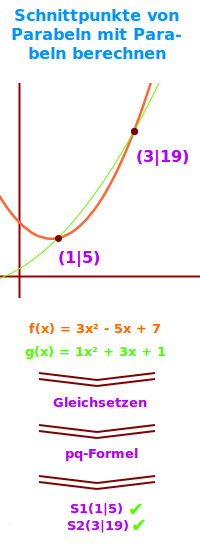Basiswissen

Lösungsidee

• Schnittpunkte sind Punkte, die gleichzeitig auf zwei Parabeln liegen.
  

• Im Schnittpunkt sind also die x- und y-Werte von beiden Parabeln gleich.
  

• Dies drückt man mathematisch durch Gleichsetzen der Gleichungen aus.
  

1. Umstellen

• 1. Man hat zwei Parabelgleichungen gegeben.
  

• 1. Beide müssen auf der linken Seite das y alleine stehen haben.
  

• 1. Statt y steht oft links auch ein f(x). Beides meint hier dasselbe.
  

• 1. Falls ein y noch nicht links alleine steht, muss man erst umstellen.
  

• 1. Parabel a gegeben: -7 = 3x² - 5x - y
  

• 1. Parabel b gegeben: y = 1x² + 3x + 1
  

• 1. Parabel a umgestellt: y = 3x² - 5x + 7
  

• 1. Parabel b umgestellt: y = 1x² + 3x + 1
  

2. Gleichsetzen

• 2. Auf beiden Seiten steht jetzt das y alleine.
  

• 2. Im nächsten Schritt setzt man die rechten Seiten gleich:
  

• 2. 3x² - 5x + 7 = 1x² + 3x + 1
  

3. Lösen

• 3. Man hat eine Gleichung mit nur noch einer Unbekannten (x).
  

• 3. Vom Typ her ist das bei Parabeln immer eine quadratische Gleichung.
  

• 3. Man bringt diese Gleichung durch Umformungen in die Normalform.
  

• 3. Die Normalform einer quadratischen Gleichung ist: 0 = x² + px + q
  

• 3. 3x² - 5x + 7 = 1x² + 3x + 1 | -1x² | -3x | -1
  

• 3. 2x² - 8x + 6 = 0 | :2
  

• 3. x² - 4x + 3 = 0 | Seiten tauschen
  

• 3. 0 = x² - 4x + 3 = 0
  

• 3. Jetzt die pq-Formel benutzen (geht immer):
  

• 3. Die Lösungen sind dann:
  

• 3. x = 1
  

• 3. x = 3
  

4. y-Werte bestimmen

• 4. Mit der pq-Formel hat man die x-Werte der Schnittpunkte bestimmt.
  

• 4. Jetzt braucht man noch die y-Werte der Schnittpunkte.
  

• 4. Dazu setzt man jeden x-Wert in eine der beiden Anfangsgleichungen ein.
  

• 4. Es ist egal, welche der beiden Gleichungen man nimmt.
  

• 4. Mit beiden kommen dieselben y-Werter heraus.
  

• 4. Hier nehmen wir Parabel, da sie einfacher ist:
  

• 4. Parabel b: y = 1x² + 3x + 1
  

• 4. Man setzt nacheinande die gefunden x-Werte in.
  

• 4. x=1 einsetzen: y = 1·1² + 3·1 + 1 gibt: y = 5
  

• 4. x=3 einsetzen: y = 1·3² + 3·3 + 1 gibt: y = 19
  

• 4. Ein x- und ein y-Wert zusammen sind dann ein Schnittpunkt.
  

• 4. Man hat also als Schnittpunkte bestimmt:
  

• 4. S1 (1|5)
  

• 4. S2 (3|19)
  

Besonderheiten

• Liefert die pq-Formel nur eine Lösung, gibt es nur einen Schnittpunkt.
  

• Liefert die pq-Formel keine Lösung, gibt es keine Schnittpunkte.
  

• Fällt mit dem Gleichsetzen das x-quadrat weg, gibt es nur einen Schnittpunkt.
  

• Man löst dann die lineare Gleichung nach x auf.