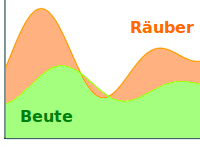
Räuber-Beute-Beziehung
Mathematisch
© 2016
- 2026
Basiswissen
Je mehr Beutetiere es gibt, desto mehr, desto mehr Räubertiere wird es bald darauf geben. Aber auch umgekehrt: wenn die Beute zurückgeht, geht kurz darauf auch die Anzahl der Räuber zurück. Wie kann man diese Beziehung rechnerisch fassen?
Beispiele
Steigt aus irgendeinem Grund die Anzahl von Fischen im Meer, steigt kurz darauf auch die Anzahl der Haie. Und: steigt die Anzahl von Schildläusen in Zitrusplantagen, dann steigt kurz darauf oft auch die Anzahl von Marienkäfern (Lausfresser). Mehr dazu unter 👉 Räuber-Beute-Beziehungen
Zusammenhang
Der kausale Zusammenhang lässt sich gut auf einem gemeinsamen Diagrammm mit der Zeit als x-Achse erkennen. Der Bestand an Beutetieren ist dabei f(x), der Bestand an Raubtieren g(x). Die Räuberkurve g(x) scheint dann gegenüber der Beutekurve f(x) etwas nach rechts verschoben zu sein.
Funktionsbeispiel
- Man modelliert die Anzahl Beutetiere als f(x).
- Die Anzahl der Räubertiere wird modelliert als g(x):
- f(x) = sin(x) + 1 + sin(1.5x - 0.4) + 2
- g(x) = 0.4 (sin(x - 0.8) + 1 + sin(1.5 (x - 0.8) - 0.4) + 4)
- g(x) ist f(x) um zwei nach oben verschoben, ...
- um 0,6 nach rechts verschoben und ...
- mit 0,4 gestaucht.