Hoch- und Tiefpunkte
Zweidimensional ist eine Funktion genau dann, wenn sie exakt zwei unabhängige Variablen hat. Ein Beispiel ist die Funktion f(x;y)=x²+y². Ihr Graph wird in einem 3D-Koordinatensystem mit x-, y- und z-Ache dargestellt. Der Graph ist hier eine nach oben geöffnete Schüssel mit dem tiefsten Punkt bei (0|0|0). Dieser Punkt ist also ein zweidimensionaler Tiefpunkt. Analog fasst man auch einen zweidimensionalen Hochpunkt. Lies mehr unter => zweidimensionale Extrempunkte berechnen
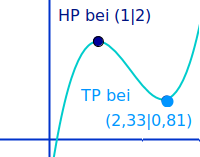Extrempunkte
Arten
Extrempunkte sind per Definition nur: Hochpunkte und Tiefpunkte. Hier werden kurz verschiedene Arten (lokal, relative, global, absolut) vorgestellt. => Ganzen Artikel lesen …
… es gibt verschiedene => zweidimensionale Extrempunkte
Hoch- oder Tiefpunkte von flächenartigen Graphen
Mehrdimensional nennt man Funktionen mit mehr als einer unabhängigen Variablen, zum Beispiel: f(x;y)=x²+y². Der Graph solcher Funktionen kann oft (nicht immer) als Fläche in einem 3D-Koordinatensystem mit x-, y- und z-Achse dargestellt werden. Die Flächen sind oft wellig, gewölbt oder parabelartig. Sie haben oft erkennbare Hoch- und Tiefpunkte. Hoch- und Tiefpunkte fasst man zusammen zu Extrempunkten. Mehrdimensionale Extrempunkte sind also Hoch- oder Tiefpunkte von Funktionen, deren Graph z. B. als Fläche dargestellt werden kann. Anschaulich handhabbar ist das nur für zweidimensionale Funktionen. Lies mehr unter => zweidimensionale Extrempunkte
… wie z. B. (4|2|Siehe unter => 3D-Punkt
Kurzanleitung für f(x;y)
Zweidimensional nennt man Funktionen mit zwei unabhängigen Variablen. Ihre Graphen sind oft Flächen in einem 3D-Koordinatensystem mit x-, y- und z-Achse. Sie zu berechnen heißt, ihre x- und y-Werte zu rechnerisch zu bestimmen. Das Vorgehen ähnelt stark dem eindimensionaler Funktion mit f(x). Das Vorgehen ist hier kurz erläutert. => Ganzen Artikel lesen …
