Windschiefe Geraden
Vektorrechnung
Geraden, die sich nie treffen und auch nicht parallel sind: in der Vektorrechnung nennt man zwei Geraden genau dann windschief, wenn keinen gemeinsamen Schnittpunkt haben und auch nicht parallel zueinander sind. Das ist gleichbedeutend mit der Aussage, dass sie auch nicht in einer gemeinsamen Ebene liegen können. => Ganzen Artikel lesen …
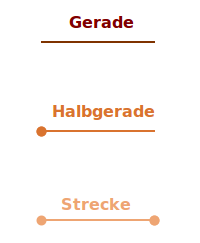Geraden
In der Mathematik: Klassifizierung und Arten
In der Mathematik werden Geraden sowohl innerhalb der Geometrie (2D und 3D) als auch in der Funktionen- und Gleichungslehre behandelt. In der Anylsis spielen sie als Veranschaulichung von linearen Funktionen (Geradengleichung) eine grundlegende Rolle. Es folgen jetzt verschiedene Typen von Geraden. => Ganzen Artikel lesen …
… es müssen mindesten zwei sein, siehe unter => windschiefe Geraden
Vektorrechnung
Das Konzept der Windschiefe lässt sich auf Ebenen in einem dreidimensionalen Raum nicht sinnvoll anwenden: zwei Ebenen können zueinander parallel, identisch, orthogonal oder schräg sein. Wenn sie aber nicht echt parallel zueinander sind, dann haben sie immer automatisch eine Schnittgerade. Das Wort windschief aber beinhaltet, dass zwei Objekte weder parallel sind noch einen Schnittpunkt haben. Daraus ergibt sich, dass es windschiefe Ebenen in einem normalen 3D-Koordinatensystem (eukdlidische Geometrie) nicht geben kann. Denkbar sind windschiefe Ebenen aber im Falle einer sogenannten => Raumkrümmung
Vektorrechnung
Das Konzept der Windschiefe lässt sich auf Vektoren in einem euklidischen Raum nicht wirklich sinnvoll anwenden. Windschief würde heißen, dass die Vektoren weder parallel zueinander sind noch einen Schnittpunkt haben. Da Vektoren aber keine Ortslage haben, haben sie auch keinen eindeutigen Schnittpunkt. Einen Ausnahme bilden Vektoren die man im Raum fest verortet. Hier könnte man das Konzept der Windschiefe sinngemäß von Geraden übertragen, was aber unüblich ist und keinen praktischen Nutzen hat. Siehe auch => windschief
