Sphärisches Dreieck
Anschaulich
Ein Dreieck auf eine Kugeloberfläche gezeichnet: wählt man drei verschiedene Punkte auf einer Kugeloberfläche aus, dann kann man diese durch möglichst kurze Linien auf der Kugeloberfläche verbinden. Das so entstandene Dreieck nennt man ein sphärisches Dreieck oder auch Kugeldreieck. Das dazugehörige Gebiet der Mathematik ist die sphärische Geometrie. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
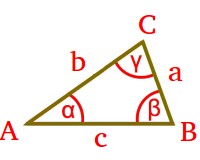Dreieck
ABC
Definition: Jede flache (2D) Figur mit genau drei Ecken und genau drei geraden Verbindungslinien zwischen den Linien ist ein Dreieck. Ein Dreieck ist damit eine Sonderfall eines Vielecks. Eine Themenübersicht steht auf der Seite => Dreiecksrechnung
… ein denkbares Zweieck auf eine Kugel, siehe unter => Kugelzweieck
Auf einer Kugeloberfläche
Sphärisch nennt man ein Viereck auf einer Kugeloberfläche gedacht: Vierecke sind per Definition immer flache Gebilde. Zwischen genau vier Ecken müssen immer Verbindungslinien liegen. Man nennt eine Strecke gerade, wenn sie die kürzsteste Verbindungsinie zwischen ihren Randpunkten ist. Man hat aber diesen Vierecksbegriff erweitert um die sogenannten sphärischen Vierecke. => Ganzen Artikel lesen …
Sphärischer Kreis
Geometrie
Ein Kreis ganz auf eine Kugeloberfläche gezeichnet: in Anlehnung an ein sogenanntes sphärisches Dreieck [1] kann man auch andere Objekte als sphärisch bezeichnen, die ganz auf einer Kugeloberfläche liegend gedacht sind. Das Besondere bei einem solchen Kreis ist, dass auch der Kreisradius und der Kreisdurchmesser ganz auf der Kugeloberfläche gedacht werden. Das hat einige interessante Konsequenzen, die hier kurz angedeutet sind. => Ganzen Artikel lesen …
… Dreieck mit einfachen Zahlen, mehr unter => pythagoreisches Tripel
