−A=Aᵀ
−A=Aᵀ: als schief- oder antisymmetrische bezeichnet man eine Matrix A, die gleich dem negativen ihrer transponierten Matrix Aᵀ ist. Transponiert heißt eine Matrix, wenn man ihre Spalten zu Zeilen gemacht. Man erkennt eine schiefsymmetrische Matrix daran, dass a) die Hauptdiagonale nur aus Nullen besteht und b) daran dass die Hauptdiagonale (oben links nach unten rechts) eine Art Symmetrieachse bildet: die gespiegelten Werte sind zueinander vom Betrag her identisch, unterscheiden sich aber immer durch ihr Vorzeichen. Das Dreieck oben rechts besteht dann sozusagen aus den Gegenzahlen der Werte des Dreiecks unten links. => Ganzen Artikel lesen …
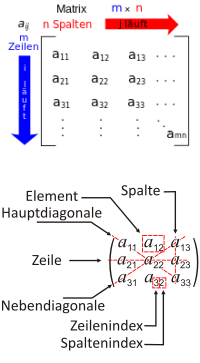Matrix
Mathematik
Kurzdefinition: eine Matrix ist eine tabellartige Anordnung von Elementen, meist von Zahlen. Mit Matrizen kann man dann verschiedene Rechnungen durchführen [1], so als sei die ganze Matrix eine Zahl. => Ganzen Artikel lesen …
… siehe unter => schiefsymmetrische Matrix
Symmetrische Matrix
Physik
Als symmetrisch bezeichnet man jede Matrix für die ihre Einträge spiegelsymmetrisch zur Hauptdiagonalen sind. Die Hauptdiagonale geht von oben links nach unten rechts. Die Einträge der Hauptdiagonalen können beliebig sein. => Ganzen Artikel lesen …
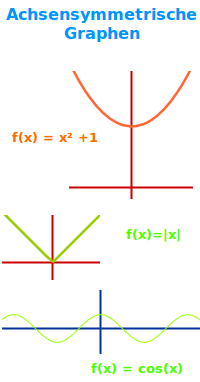
Achsensymmetrische Graphen
Beispiele
Funktionen, deren Graph achsensymmetrisch zur y-Achse ist nennt man oft kurz achsensymmetrisch. Von der Form erscheinen sie oft schmetterlingsartig. Es gibt aber viele andere Formen. Hier stehen einige Beispiele. Eine ausführliche Erklärung steht auf der Seite zur => Achsensymmetrie von Graphen
Stochastische Matrix
Definition
Eine stochastische Matrix ist ein Recheninstrument für Zufallsprozesse. Man kann damit schrittweise von einem Zustand zum nächsten in die Zukunft oder auch in die Vergangenheit rechnen. Der theoretische Hintergrund wird erläutert auf => Stochastische Prozesse (Matrizenrechnung)
