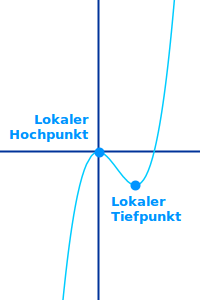
Lokaler Extrempunkt
Definition
Zu den Extrempunkten gehören nur Hoch- und Tiefpunkte. Ein lokaler Extrempunkt ist in seiner Umgebung der höchste oder tiefste Punkt. Umgebung meint: beliebig nah links und rechts an diesem Punkt. Anders gesagt: es muss eine Umgebung geben - egal wie klein in der kein Punkt höher oder tiefer ist als dieser Punkt. Siehe auch => Lokale Extrempunkte bestimmen
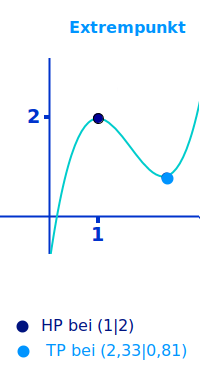Extrempunkt
Definition
Zu den Extrempunkten von Funktionen f(x) zählen nur Hoch- und Tiefpunkte. Man kann Extrempunkte über die erste Ableitung f'(x) und die zweite Ableitung f''(x) bestimmen. Aber mit der schulüblichen Definition der Extrempunkte ergeben sich zwei Probleme, die hier kurz besprochen (und gelöst) werden. => Ganzen Artikel lesen …
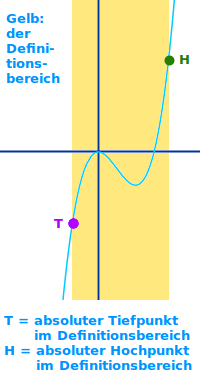Globaler Extrempunkt
Analysis
Es gibt keinen höheren oder tieferen Punkt: ein Punkt auf einem Funktionsgraphen, für den es keinen höheren oder tieferen Punkt sonstwo auf dem Graphen gibt ist ein globaler Extrempunkt. => Ganzen Artikel lesen …
… Definition unter => lokaler Extrempunkt
… Hoch- und Tiefpunkte, Definition unter => globaler Extrempunkt
