Übersicht
Funktionen wie f(x)=4x+5 oder f(x)=x²-1 werden nach verschiedenen Kriterien klassifiziert. Einige der wichtigsten werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Beispiele
Nicht lineare sind zum Beispiel quadratische oder Wurzelfunktionen. Und obwohl der Graph auch eine Gerade ist, gehören auch konstante Funktionen oder Geraden parallel zur y-Achse nicht zu den linearen Funktionen. => Ganzen Artikel lesen …
Beispiele
Elementar nennt man jede Funktion, die sich entweder nicht weiter in einfachere Funktionen zerlegen lässt oder deren Funktionswerte in einer endlichen Anzahl von Schritten berechnet werden können [1]. Dazu stehen hier Beispiele. => Ganzen Artikel lesen …
Lineare Funktionen
Beispiele
Linear nennt man jede Funktion, deren Gleichung man in die Form f(x)=ax+b oder f(x)=mx+b bringen kann. Der Graph einer linearen Funktion ist immer eine Gerade. Die Funktionsgleichung einer linearen Funktion ist immer eine Geradengleichung. Es folgen einige Arten und Beispiele. Eine Übersicht zum gesamten Thema steht auf => lineare Funktion
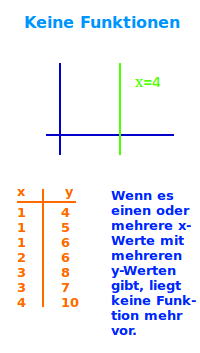
Keine Funktionen
Beispiele für Zuordnungen, die aber keine Funktionen sind
Wenn zu einem x-Wert mehrere y-Werte gehören, dann liegt keine Funktion sondern nur noch eine Relation (Zuordnung) vor. Hier einige Beispiele dazu. => Ganzen Artikel lesen …
