… siehe unter => erweiterte Exponentialfunktion aus zwei Punkten
Das Verfahren zur Erstellung der Expoentialgleichung ist analog zu dem der Erstellung einer Exponentialfunktion. Bei Gleichungen schreibt man tendenziell eher y und bei Funktionen eher f(x). Der Bedeutungsunterschied ist für das Verfahren unwichtig. Mehr unter => erweiterte Exponentialfunktion aus zwei Punkten
Definition: die Unbekannte kommt im Exponenten vor
2 hoch 3x-9 = 64: eine Gleichung, bei der das x, das heißt die Unbekannte, im Exponenten steht heißt Exponentialgleichung [1]. Die Lösung im Beispiel ist x=5. => Ganzen Artikel lesen …
Zwei
Als Zahl
Die Zwei ist die nächst natürliche Zahl nach der Eins. Das Zweifache nennt man auch das Doppelte. Als Hochzahl spricht man die Zwei auch als Quadrat aus: 3² ist 3 hoch 2 oder 3 quadrat. Hier stehen einige Besonderheiten zur Zahl Zwei. => Ganzen Artikel lesen …
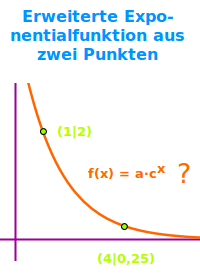Erweiterte Exponentialfunktion aus zwei Punkten
f(x)=a·bˣ
Man hat zwei oder mehr Punkte eines Graphen von einer Exponentialfunktion. Mit diesen Angaben kann man eine Funktionsgleichung erstellen. Gesucht sind die Koeffizienten a und b. Für sie sollen am Ende konkrete Zahlenwerte eingesetzt werden. Das Verfahren verläuft analog zum aufstellen einer Geradengleichung oder einer Parabelgleichung aus zwei Punkten: man setzt beide Punkte in die Grundform (Bauplan) der Funktionsgleichung ein. Dadurch ensteht ein lineares Gleichungssystem (LGS), das man dann löst. Die Ergebnisse des LGS sind die gesuchten Koeffizienten des Funktionstermes. Das Dach ^ steht für hoch. b^x meint dasselbe wie b-hoch-x. => Ganzen Artikel lesen …
Anleitungen
y = a·b^x oder als Funktionsgleichung auch z. b. B(x) = a·q^x oder ähnliche Darstellungsformen nennt man die erweiterte Exponentialgleichung oder erweiterte Exponentialfunktion. Man kann sie nach jedem ihrer Bausteine umstellen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… y=a·b^x, siehe unter => erweiterte Exponentialgleichung aus zwei Punkten
