Einfache Exponentialfunktion
f(x) = a^x
Bei der einfachen Exponentialfunktion gibt es nur eine Basis hoch der Variablen (meist x). Zu diesem Term wird nichts hinzuaddiert oder er wird auch nicht mit irgendwas malgenommen. Wird der Term über weitere Rechenarten erweitert, entsteht die sogennante => erweiterte Exponentialfunktion
Einmal irgendwas
Das Einfache von 4 ist 4: das Einfache heißt, dass man etwas genau 1 mal hat. Das Wort ist ähnlich wie das Doppelte oder das Dreifache. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
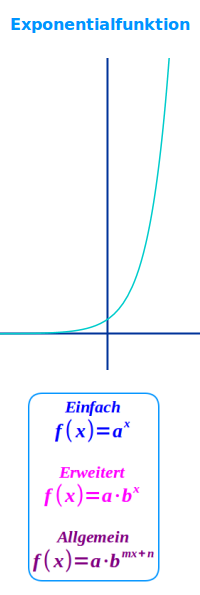
Exponentialfunktion
Funktion mit x im Exponenten
Jede Funktion, die sich umformen lässten in f(x) = a·b^T(x) heißt Exponentialfunktion. Das T(x) ist irgendein Term, bei dem eines oder mehrere x'se vorkommen. Bei einer Exponentialfunktion kommt immer ein x in einem Exponenten vor, daher auch der Name. Ist die Basis b der Potenz die Eulersche Zahl e, spricht man auch von einer e-Funktion. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Graph einer hoch-x-Funktion => Exponentialkurve
Einfache Exponentialkurve
Graph
f(x) = a^x: dies ist die einfache oder elementare Exponentialfunktion. Ihr Graph ist die einfache Exponentialkurve. Hier stehen Eigenschaftten des Graphen => Ganzen Artikel lesen …
… f(x) = a^x, siehe unter => einfache Exponentialfunktion
Einfache Exponentialfunktion ableiten
f(x) = a^x abgeleitet gibt f'(x) = ln(a)·a^x
Die einfache Exponentialfunktion besteht aus einer Konstanten als Basis einer Potenz und dem x als Exponent dieser Potenz. Es dürfen keine weiteren Zahlen oder Rechnungen damit verbunden sein. => Ganzen Artikel lesen …
… meint dasselbe wie die => e-Funktion
… a^x abgeleitet gibt a^x·ln(a) => Ableitungsregeln
Erklärung am Beispiel der Punkte (2|9) (5|243)
Hat man zwei Punkte gegeben, dann kann es sein, dass es gar keine Exponentialfunktion gibt, die durch beide Punkte geht. Um herauszufinden, ob es doch geht und wie dann die Funktionsgleichung aussieht, kannst du immer so vorgehen: => Ganzen Artikel lesen …
