Wurzel

Definition

Die Wurzel von der Zahl 16 ist die 4. Denn: 4 mal 4 gibt wieder 16. Man schreibt kurz: √16=4. Die Wurzel von irgendeiner Zahl z ist diejenige nicht negative Zahl, die mit sich selbst malgenommen wieder die Zahl ergibt. Diese Definition gilt für die umgangssprachlich gesprochen „normale“ Wurzel, die man auch Quadratwurzel nennt. => Ganzen Artikel lesen …

3: Worfeln

… siehe unter => Windsichten

Würfeln

Spielen, Kochen

Würfeln kann heißen, dass man einen Spielwürfel wirft. Würfeln, etwa in einem Kochrezept, kann auch bedeuten, dass man etwas in viele Würfeln teilt (z. B. Käse). Hier wird kurz das Würfeln aus Sicht der Mathematik vorgestellt. => Ganzen Artikel lesen …

5: Wurzel z

… Definition unter => Wurzel einer komplexen Zahl

7: Abnormale Wurzeln

… alle außer den Quadratwurzeln, mehr unter => Wurzelarten

8: Addition von Quadratwurzeln

… es gibt keine Regel, mehr unter => Wurzel plus Wurzel

9: Addition von Wurzeln

… siehe => Wurzel plus Wurzel

10: Addition Wurzeln

… siehe => Wurzel plus Wurzel

11: Babylonisches Wurzeln

… Schritt-für-Schritt Anleitung unter => Heron-Verfahren

12: beliebige Wurzeln

… wie etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel

13: Bruch mit Wurzeln

… siehe unter => Wurzel durch Wurzel

14: Bruch wurzeln

… siehe unter => Wurzel aus Bruch

15: Bruchrechnung mit Wurzeln

… 4/9 wird zu 2/3 => Wurzel aus Bruch ziehen

16: Brüche und Wurzeln

… 4/9 wird zu 2/3 => Wurzel aus Bruch ziehen

17: Brüche wurzeln

… siehe unter => Wurzel aus Bruch

18: Division von Quadratwurzeln

… kann man oft vereinfachen, siehe unter => Wurzeln dividieren

19: Division von Wurzeln

… kann man oft vereinfachen, siehe unter => Wurzeln dividieren

20: Division Wurzeln

… kann man oft vereinfachen, siehe unter => Wurzeln dividieren

21: Dritte Wurzeln

… Zahlenliste mit über 1000 Werten unter => Kubikwurzeln

22: Funktionen Wurzeln

… Funktion mit Wurzel, mehr unter => Wurzelfunktion

23: Graphisch wurzeln ziehen

… rein textliche Beschreibung unter => Wurzelschnecke

24: Hochrechnen mit Wurzeln

… wie etwa (Wurzel 4)³, siehe unter => Wurzel potenzieren

25:

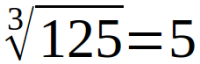Kubikwurzeln

Liste 1000

Die Kubikwurzel von 27 ist 3 und die Kubikwurzel von 8 ist 2. Hier steht eine längere Liste. => Ganzen Artikel lesen …

26: Kubikwurzeln berechnen

… z. B. aus der 8 die 2, siehe unter => Kubikwurzel ziehen

27: Kubikwurzeln bestimmen

… z. B. aus der 8 die 2, siehe unter => Kubikwurzel ziehen

28: Minuswurzeln

… gibt es nicht, mehr unter => Negative Wurzel

29: Multiplikation von Quadratwurzeln

… kann man oft vereinfachen, siehe unter => Wurzeln multiplizieren

30: Multiplikation von Wurzeln

… kann man oft vereinfachen, siehe unter => Wurzel mal Wurzel

31: Multiplikation Wurzeln

… kann man oft vereinfachen, siehe unter => Wurzeln multiplizieren

33: n-zahligste Wurzeln

… wie etwa die 4-te Wurzel, siehe unter => n-te Wurzel

34: negative Wurzeln

… gibt es nicht, mehr unter => Negative Wurzel

35: Potenz von Wurzeln

… wie etwa (Wurzel 4)³, siehe unter => Wurzel potenzieren