Wurzelfunktion

Jede Funktion, bei der x nur unter einer Wurzel vorkommt

Man unterscheidet eine Wurzelfunktion im engeren Sinn, oft „Die Wurzelfunktion“ oder „einfache Wurzelfunktion“ genannt, und eine Wurzelfunktion im Allgemeinen Sinn. => Ganzen Artikel lesen …

3: Winkelfunktion

… siehe unter => trigonometrische Funktion

4: Areafunktion

… Eine Umkehrfunktion einer Hyperbelfunktion, siehe auch => Areafunktionen [Liste]

5: Wurzel in Funktion

… Funktion mit Wurzel, mehr unter => Wurzelfunktion

Die Wurzelfunktion

… die Wurzelfunktion im engeren Winn, auch => einfache Wurzelfunktion

8: Ableitung Wurzelfunktion

… f(x)=√x ⭢ f'(x) = -½·x^(-0,5) => Wurzelfunktion ableiten

10: Die einfache Wurzelfunktion

… f(x) = Wurzel von x, mehr unter => einfache Wurzelfunktion

11:

Einfache Wurzelfunktion

f(x)=√x: Die Wurzelfunktion im engeren Sinn

Die einfache oder auch elementare Wurzelfunktion hat die Form f(x)=√x. Sie ist nicht definiert für negative Zahlen. Ihr Graph hat die Form einer querliegenden Parabelastes. => Ganzen Artikel lesen …

12: Elementare Wurzelfunktion

… f(x) = Wurzel x, siehe unter => einfache Wurzelfunktion

13: Erste Ableitung der Wurzelfunktion

… f(x)=√x ⭢ f'(x) = -½·x^(-0,5) => Wurzelfunktion ableiten

14: Erste Ableitung von Wurzelfunktion

… f(x)=√x ⭢ f'(x) = -½·x^(-0,5) => Wurzelfunktion ableiten

15: Erste Ableitung Wurzelfunktion

… f(x)=√x ⭢ f'(x) = -½·x^(-0,5) => Wurzelfunktion ableiten

16: Graph der Wurzelfunktion

… ist parabelförmig aber gedreht und heißt => Wurzelkurve

17: Graph einer Wurzelfunktion

… ist parabelförmig aber gedreht und heißt => Wurzelkurve

18: Graph von Wurzelfunktion

… siehe unter => Wurzelkurve

19: Kurve der Wurzelfunktion

… ist parabelförmig aber gedreht und heißt => Wurzelkurve

20: Wurzelfunktion abgeleitet

… √x abgeleitet gibt 0,5/√x => Wurzelfunktion ableiten

21:

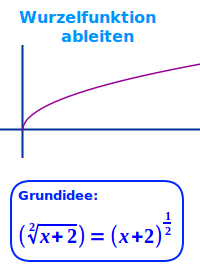22: Wurzelfunktion als Graph

… ist parabelförmig aber gedreht und heißt => Wurzelkurve

23: Wurzelfunktion Graph

… ist parabelförmig aber gedreht und heißt => Wurzelkurve

24: Wurzelfunktionengraf

… siehe unter => Wurzelkurve

25: Wurzelfunktionengraph

… siehe unter => Wurzelkurve

26: Wurzelfunktionsgraf

… ist parabelförmig aber gedreht und heißt => Wurzelkurve

27: Wurzelfunktionsgraph

… ist parabelförmig aber gedreht und heißt => Wurzelkurve

28: Wurzelfunktionskurve

… ist parabelförmig aber gedreht und heißt => Wurzelkurve