Länge der Randlinie
Kreis, Quadrate, Rechtecke, Rauten und so weiter: für grundlegende geometrische Formen verwendet man Standardformeln. => Ganzen Artikel lesen …
 Umfang
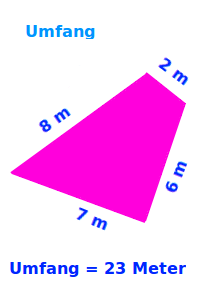
Umfang
Eine Rand- beziehungsweise Umfangslinie
Definition: Man hat eine ebene (flache Figur), die durch eine durchgehende Linie begrenzt ist. Diese Linie nennt man die Rand- oder Umfangslinie. Ihr Länge wird kurz als Umfang bezeichnet. Die übliche Abkürzung ist ein großes U. => Ganzen Artikel lesen …
 Berechnen
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… Formeln unter => Umfang berechnen
… Formeln unter => Umfang berechnen
… Formeln unter => Umfang berechnen
… Die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… Formel und Herleitung unter => Kreisfläche aus Kreisumfang
 Kreisumfang berechnen
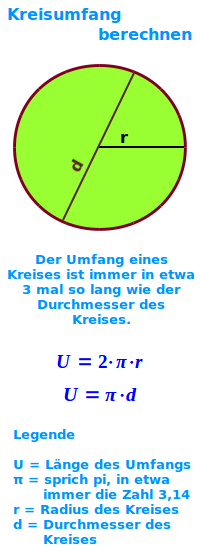
Kreisumfang berechnen
Übersicht
U = 2·π·r oder Umfang = pi mal Durchmesser oder zwei mal pi mal Radius: der Kreisumfang U ist die Länge der Kreislinie (also des Kreisrandes). Er wird oft mit einem großen U abgekürzt. Man kann den Umfang berechnen, wenn man entweder den Radius r, den Durchmesser d oder den Flächeninhalt A kennt. Alle drei Varianten werden hier kurz erklärt. => Ganzen Artikel lesen …
Kugelumfang gleich Pi mal Durchmesser
Der Umfang einer Kugel ist die Länge des größtmöglichen Kreises auf der Kugeloberfläche. Die Länge ist immer => Ganzen Artikel lesen …
Anleitung
Ein Quadrat hat vier gleich lange Seiten. Rechne die Längen der vier Seiten zusammen. Das Ergebnis ist der Quadratumfang. Dazu steht hier kurz ein Beispiel vorgerechnet. => Ganzen Artikel lesen …
… Formeln unter => Umfang berechnen

