Definition: Sinus, Cosinus Tangens etc.
Der Sinus, Cosinus und Tangens wurden ursprünglich anschaulich an rechtwinkligen Dreiecken definiert. Über eine neue Definition über den Einheitskreises ist der anschauliche Bezugspunkt dann nicht mehr das rechtwinklige Dreieck sondern es sind dann periodische Vorgänge (Jahreszeiten, Schwingungen, Wirtschaftszyklen etc.). => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
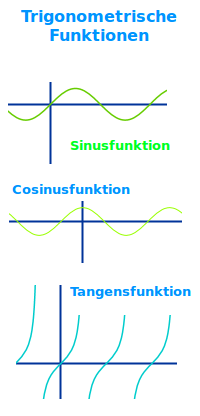
Trigonometrische Funktionen
Sinus, Cosinus, Tangens
Die grundlegenden trigonometrischen Funktionen sind die Sinus-, Cosinus- und Tangensfunktion. Sie sind oft das mathematische Modell für periodische Vorgänge wie die Sonneeinstrahlung über die Jahreszeiten. Hier werden die Funktionen kurz vorgestellt. => Ganzen Artikel lesen …
… z. B. punkt- oder Achsensymmetrisch => Funktionen nach Symmetrien
… an der y-Achse gespiegelt, mehr unter => Achsensymmetrie von Graphen
… Man sieht am besten in Formelsammlungen nach, siehe z. B. => Ableitungen
Als trigonometrische Funktionen fasst man im Wesentlichen f(x)=sin(x), f(x)=cos(x) und f(x)=tan(x) zusammen. Darüberhinaus gibt es weitere trigonometrische Funktionen und viele abgewandelte Formen. Neben den Grundableitungen gibt es zahlreiche Sonderfälle, die in Formelsammlungen zusammgenstellt sind. Die Grundableitung sind:
