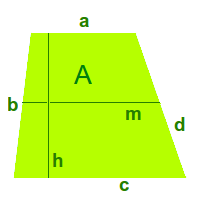
Trapezfläche berechnen
Anleitung
Zum Beispiel in cm² oder m²: die Trapezfläche A kann auf verschiedene Arten berechnet werden. Ein Trapez hat immer mindestens zwei Seiten die sich gegenüber liegen und parallel zueinander sind. Neben den Formeln gibt es auch die Möglickeit der Zerlegung der Fläche in Teilflächen. Beide Varianten werden hier kurz vorgestellt. => Ganzen Artikel lesen …
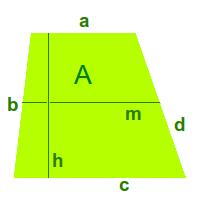Trapezfläche
Definition
Ein Trapez ist ein Vierecke mit mindestens zwei zueinander parallelen Seiten. Die Fläche kann sowohl die Fläche selbst als auch ihren Inhalt, z. B. in cm² oder m² meinen. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
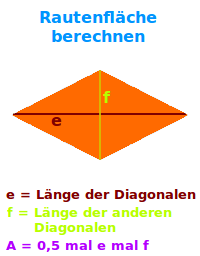Rautenfläche berechnen
A = 0,5 mal e mal f
Länge e der einen Diagonalen mal Länge f der anderen Diagonalen und das Zwischenergebnis geteilt durch zwei ergibt den Flächeninhalt A der Raute. => Ganzen Artikel lesen …
Anleitung
Drei verschiedene Formeln zur Berechnung der Höhe h eines Trapezes. Die Formeln sind hier kurz mit ausführlicher Legende vorgestellt. => Ganzen Artikel lesen …
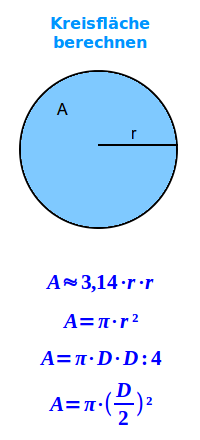Kreisfläche berechnen
A = π·r²
Pi (etwa 3,14) mal den Radius mit sich selbst malgenommen. Beispiel: für den Radius r = 2 Meter rechnet man: 3,14·2·2 = 12,56 m². Das ist die einfachste Formel. Daneben gibt es noch weitere. Diese werden hier kurz vorgestellt. => Ganzen Artikel lesen …
… für die Flächenberechnung, siehe unter => Trapezfläche über zerlegen
