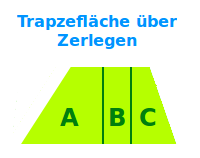
Trapezfläche über Zerlegen
Anleitung
Ein Trapez ist ein Viereck mit mindestens zwei zueinander parallelen Seiten. Ein Trapez kann immer in Dreiecke und Rechtecke zerlegt werden. Darüber lässt sich der Flächeninhalt auch ohne spezielle Trapezformel mit einfachen Grundformeln (elementar) berechnen. Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …
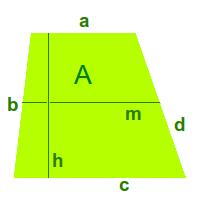Trapezfläche
Definition
Ein Trapez ist ein Vierecke mit mindestens zwei zueinander parallelen Seiten. Die Fläche kann sowohl die Fläche selbst als auch ihren Inhalt, z. B. in cm² oder m² meinen. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Zerlegen
Mathematik
Definition: Zahlen, Formen, Mengen oder Gegenstände: etwas zu zerlegen heißt in der Mathematik: Einzelteile daraus machen, die man gedanklich wieder zum Ganzen zusammensetzen könnte. Die Größe oder Form der Einzelteile ist dabei unwichtig. => Ganzen Artikel lesen …
… für die Flächenberechnung, siehe unter => Trapezfläche über zerlegen
… für die Flächenberechnung, siehe unter => Trapezfläche über zerlegen
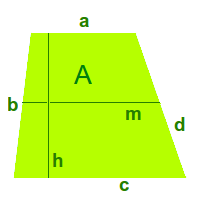Trapezfläche berechnen
Anleitung
Zum Beispiel in cm² oder m²: die Trapezfläche A kann auf verschiedene Arten berechnet werden. Ein Trapez hat immer mindestens zwei Seiten die sich gegenüber liegen und parallel zueinander sind. Neben den Formeln gibt es auch die Möglickeit der Zerlegung der Fläche in Teilflächen. Beide Varianten werden hier kurz vorgestellt. => Ganzen Artikel lesen …
… für die Flächenberechnung, siehe unter => Trapezfläche über zerlegen
… In zwei Dreiecke und ein Rechteck => Trapezfläche über zerlegen
