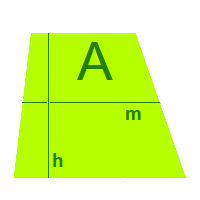
Trapezfläche über m und h
Berechnung
Die Berechnung des Flächeninhaltes eines Trapezes über die Mittellinie wird hier kurz erklärt. Jedes Viereck, bei dem mindestens zwei Seiten zueinander parallel sind nennt man ein Trapez. => Ganzen Artikel lesen …
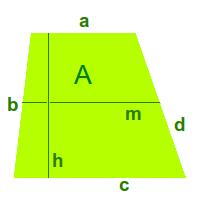Trapezfläche
Definition
Ein Trapez ist ein Vierecke mit mindestens zwei zueinander parallelen Seiten. Die Fläche kann sowohl die Fläche selbst als auch ihren Inhalt, z. B. in cm² oder m² meinen. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Akbürzung
Das kleine m oder das große M als Abkürzung: hier stehen verschiedene Bedeutungen aus der Mathematik, Physik und Chemie. => Ganzen Artikel lesen …
Logisches UND
x=3 UND x=4 heißt: x soll gleichzeitig 3 und 4 sein. Das ist ein logischer Widerspruch. Besser ist oft das logische ODER: Möchte man beispielweise als zwei Lösungen einer pq-Formel angeben, dass einmal x=3 und einmal x=4 als Lösung gilt, dann schreibt man: x=3 ODER x=4; kurz: x=3 v x=4. Lies mehr unter => Logisches UND
Bedeutungen
Als kleines h oder als großes H: der lateinische Buchstabe kann für verschiedene Dinge stehen, hier stehen Beispiele aus der Mathematik und den Naturwissenschaften. => Ganzen Artikel lesen …
… A=0,5*(a+c)Siehe unter => Trapezfläche über m und h
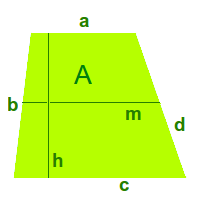Trapezfläche berechnen
Anleitung
Zum Beispiel in cm² oder m²: die Trapezfläche A kann auf verschiedene Arten berechnet werden. Ein Trapez hat immer mindestens zwei Seiten die sich gegenüber liegen und parallel zueinander sind. Neben den Formeln gibt es auch die Möglickeit der Zerlegung der Fläche in Teilflächen. Beide Varianten werden hier kurz vorgestellt. => Ganzen Artikel lesen …
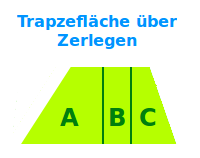Trapezfläche über Zerlegen
Anleitung
Ein Trapez ist ein Viereck mit mindestens zwei zueinander parallelen Seiten. Ein Trapez kann immer in Dreiecke und Rechtecke zerlegt werden. Darüber lässt sich der Flächeninhalt auch ohne spezielle Trapezformel mit einfachen Grundformeln (elementar) berechnen. Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …
… für die Flächenberechnung, siehe unter => Trapezfläche über zerlegen
