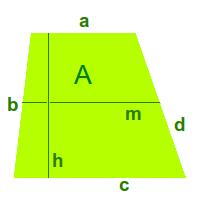
Trapezfläche
Definition
Ein Trapez ist ein Vierecke mit mindestens zwei zueinander parallelen Seiten. Die Fläche kann sowohl die Fläche selbst als auch ihren Inhalt, z. B. in cm² oder m² meinen. => Ganzen Artikel lesen …
Formel
Zum Beispiel: A=a·b
Eine Formel in der Mathematik ist ein möglichst kurz mit Symbolen geschriebener Satz oder eine Aussage. [1] In der Chemie geben Formeln die Zusammensetzung von Verbindungen an. Der Name kommt daher, da eine Formel angibt, in welche Form ihre Bestandteile zusammen gedacht werden sollen. [6] => Ganzen Artikel lesen …
Mathematik | Physik | Chemie
a kann für ein Jahr (annum) als Einheit stehen, oder für die Beschleunigung a oder eine Seitenlänge. Diese und einige weitere Bedeutungen sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Logisches UND
x=3 UND x=4 heißt: x soll gleichzeitig 3 und 4 sein. Das ist ein logischer Widerspruch. Besser ist oft das logische ODER: Möchte man beispielweise als zwei Lösungen einer pq-Formel angeben, dass einmal x=3 und einmal x=4 als Lösung gilt, dann schreibt man: x=3 ODER x=4; kurz: x=3 v x=4. Lies mehr unter => Logisches UND
Formeln zu Berechnung des Flächeninhaltes (z. B. Quadratzentimeter)
- => Trapezfläche [normale Formel mit a und c]
… Formel für den Flächeninhalt eines Trapezes => Trapezfläche
… A=0,5*(a+c)Siehe unter => Trapezfläche über m und h
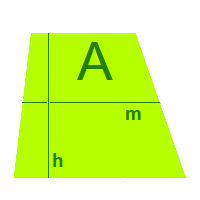Trapezfläche über m und h
Berechnung
Die Berechnung des Flächeninhaltes eines Trapezes über die Mittellinie wird hier kurz erklärt. Jedes Viereck, bei dem mindestens zwei Seiten zueinander parallel sind nennt man ein Trapez. => Ganzen Artikel lesen …
… In zwei Dreiecke und ein Rechteck => Trapezfläche über zerlegen
… für die Flächenberechnung, siehe unter => Trapezfläche über zerlegen
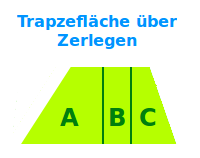Trapezfläche über Zerlegen
Anleitung
Ein Trapez ist ein Viereck mit mindestens zwei zueinander parallelen Seiten. Ein Trapez kann immer in Dreiecke und Rechtecke zerlegt werden. Darüber lässt sich der Flächeninhalt auch ohne spezielle Trapezformel mit einfachen Grundformeln (elementar) berechnen. Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …
… für die Flächenberechnung, siehe unter => Trapezfläche über zerlegen
