ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
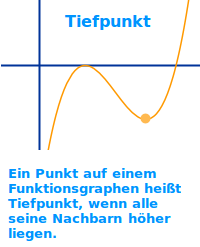
1: Tiefpunkt

Analysis

Definition: ein Tiefpunkt im Sinne der Analysis ist ein Punkt auf einem Funktionsgraphen. In der Umgebung links und rechts von diesem Punkt sind alle anderen Punkte höher. Erklärt werden verschiedene Arten von Tiefpunkten und wie man sie bestimmt. => Ganzen Artikel lesen …
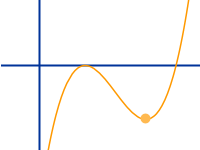2: Tiefpunkte

… Arten und Anzahlen | siehe auch => Tiefpunkte bestimmen

Innerhalb der Analysis sind Tiefpunkte die in ihrer Umgebung tiefsten Punkte eines Graphen. In ihrer Umgebung heißt, dass man einen beliebig kleinen Bereich links und rechts des Punkte angeben kann, in dem es keine gleich tiefen oder tieferen Punkte gibt. Das Fremdwort für „in der näheren Umgebung“ ist lokal. Jeder Tiefpunkt ist damit per Definition ein lokaler Tiefpunkt. Ist er darüberhinaus der überhaupt tiefste Punkt des Graphen im Definitionsbereich oder einem ausgewählten Intervall, so nennt man ihn den globalen Tiefpunkt in diesem Bereich. Verschiedene Funktionsarten können unterschiedlich viele Tiefpunkte haben. Zur weiteren Definition siehe auch unter => Tiefpunkt
3: Aufpunkt

… in der Vektorrechnung dasselbe wie ein => Stützpunkt
4: Drehpunkt

Geometrie | Graphen | Hebel

Ein Drehpunkt ist ein Punkt, um den anderen Dinge gedreht werden - gedanklich oder tatsächlich. In der Geometrie sowie bei punktsymmetrischen Graphen spricht man allgemein vom Symmetriezentrum. Bei Hebeln (Physik) ist das der Punkt, um den ein Hebel gedreht wird. Die Fälle werden hier kurz erklärt. => Ganzen Artikel lesen …
5: Siedepunkt

… Temperatur, bei der eine Flüssigkeit zu sieden anfängt => Siedetemperatur
6: Betriebspunkt

Bergbau

Im Bergbau bezeichnet ein Betriebspunkt einen räumlich festgelegten Ort, an dem bergmännische Arbeiten durchgeführt werden: ein Streckenvortrieb, ein Abbau oder eine Kippstelle [1]. Betriebspunkte wurden vor allem zur Zuordnung von anfallenden Kosten definiert, also als => Kostenstelle
7: Absolute Tiefpunkte berechnen

… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
8: Absoluten Tiefpunkt berechnen

… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
9: Absoluten Tiefpunkt bestimmen

… siehe unter => globalen Extrempunkt berechnen
10: Absoluter Tiefpunkt

Funktionsgraphen

Bei Funktionsgraphen ist der absolute Tiefpunkt, auch globaler Tiefpunkt genannt, der tiefste Punkt im gesamten Definitionsbereich. Das heißt, es gibt für die insgesamt erlaubten x-Werte keinen tieferen Punkt auf dem ganzen Graphen. Mehr dazu unter => globaler Tiefpunkt
11: Analytische Tiefpunktbestimmung

… Anleitung steht unter => Tiefpunkte über Analysis
12: Bestimmung des Tiefpunktes

… z. B. über Ableitungen, siehe unter => Tiefpunkte bestimmen
13: Bestimmung Tiefpunkt

… z. B. über Ableitungen, siehe unter => Tiefpunkte bestimmen
14: Bestimmung Tiefpunkte

… z. B. über Ableitungen, siehe unter => Tiefpunkte bestimmen
15: Bestimmung von einem Tiefpunkt

… z. B. über Ableitungen, siehe unter => Tiefpunkte bestimmen
16: Bestimmung von Tiefpunkten

… z. B. über Ableitungen, siehe unter => Tiefpunkte bestimmen
17: Erste Ableitung und Tiefpunkt

… Anleitung steht unter => Tiefpunkte über Analysis
18: Gegenteil eines Tiefpunktes

… bei einer mathematischen Kurvendiskussion ist das ein => Hochpunkt
19: Gleichung Tiefpunkt Tangente

… Definition unter => Tiefpunkttangente
20: Globale Tiefpunkte

… Beispiele unter => globale Extrempunkte
21: Globalen Tiefpunkt berechnen

Analysis

Ein globaler Tiefpunkt ist der niedrigste Punkt in einem betrachteten Intervall. Man geht meist so vor, dass man überhaupt nach Extrempunkten sucht und dann entscheidet, wer davon ein Hoch- und wer ein Tiefpunkt ist. Das ist ausfürlich erklärt im Artikel => globalen Extrempunkt berechnen
22: Globalen Tiefpunkt bestimmen

… über f'(x) und Randverhalten, siehe unter => globalen Extrempunkt berechnen
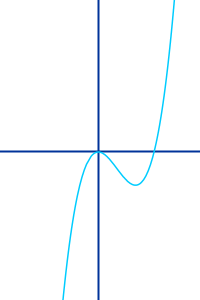23: Globaler Tiefpunkt

Analysis

Definition: alle anderen Punkte im Definitionsbereich sind höher. => Ganzen Artikel lesen …
24: Hoch- und Tiefpunkte

… In der Analysis: fasst man zusammen zu => Extrempunkte
25: Hoch- und Tiefpunkte bestimmen

… Hoch- und Tiefpunkte finden, siehe unter => Extrempunkte bestimmen
26: Hoch- und Tiefpunkte von Parabeln bestimmen

… alle Verfahren unter => Scheitelpunkt einer Parabel bestimmen
27: Keine Tiefpunkte

Beispiele

Geraden, nach unten geöffnete Parabeln oder Hyperbeln: hier stehen einige Funktionen oder Graphen, die keinen Tiefpunkt haben. => Ganzen Artikel lesen …
28: Kurvendiskussion Tiefpunkt

… Tiefpunkte über erste Ableitung, siehe => Tiefpunkte bestimmen
29: Kurvendiskussion Tiefpunkte

… Tiefpunkte über erste Ableitung, siehe => Tiefpunkte bestimmen
30: Lokale Tiefpunkte bestimmen

… Tiefpunkte über erste Ableitung, siehe => Tiefpunkte bestimmen
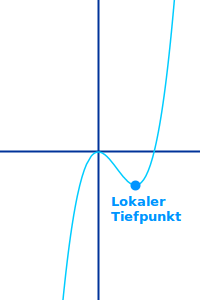31: Lokaler Tiefpunkt

Analysis

Definition: ein lokaler Tiefpunkt, auch relativer Tiefpunkt genannt, ist der tiefste Punkt in seiner Umgebung. Seine unmittelbaren Nachbarn sind alle höher als der Tiefpunkt. => Ganzen Artikel lesen …
32: Parabel mit Tiefpunkt

… Scheitelpunkt ist tiefster Punkt, mehr unter => nach oben geöffnet
33: Parabeltiefpunkt

… Zur Definition und Berechnung lies unter => Scheitelpunkt einer Parabel
34: Parabeltiefpunkt berechnen

Methoden

Der Tiefpunkt einer Parabel ist immer auch der Scheitelpunkt. Es gibt zwei Standard-Methoden, wie man die x- und y-Koordinate eines solchen Tiefpunktes berechnet. Beide Verfahren sind hier kurz vorgestellt. => Ganzen Artikel lesen …
35: Parabeltiefpunkt bestimmen

… mehrere Methoden unter => Scheitelpunkt einer Parabel berechnen
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023