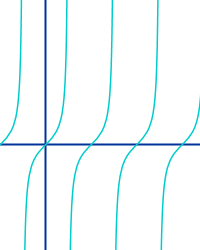
Tangensfunktion
f(x) = tan(x)
Der Graph wiederholt sich periodisch. Dabei existieren ständig wiederkehrende Definitionslücken. => Ganzen Artikel lesen …
… z. B. t(x)=4x-3, siehe unter => Tangentengleichung
Eine Tangente ist immer eine Gerade, die irgendwo einen Punkt mit einem anderen Graphen gemeinsam hat und an dieser Punkt dieselbe Steigung wie der andere Graph hat. Eine Tangente kann grundsätzlich auch eine senkrechte Linie parallel zur y-Achse sein. Eine solche Linie ist aber keine Funktion. Man spricht deshalb besser allgemein von einer => Tangentengleichung
… wie f(x)=2x+4, mehr unter => Lineare Funktion
… f(x)=tanh(Siehe unter => Tangens Hyperbolicus-Funktion
Tangens rückwärts
f(x) = arctan(x) nennt man die elementare oder einfache Arcustangensfunktion. Gibt man für x ein Zahl ein, dann erhält man als Ergebnis der Funktion den Winkel, der genau diese Zahl als Tangens hat. Hier stehen Eigenschafter dieser Funktion. => Ganzen Artikel lesen …
Einsfunktion
f(x)=1
Ordnet jedem x-Wert die Zahl 1 als Funktionswert zu. Der Graph ist eine horizontale Linie parallel zur x-Achse. => Ganzen Artikel lesen …
…(x) abgeleitet gibt 1/[cos²(x)], sprich Eins-durch Cosinus-quadrat-x
…(x) abgeleitet gibt 1/[cos²(x)], sprich Eins-durch Kosinus-quadrat-x
… gibt 0, mehr unter => 0 aufgeleitet
…(x) abgeleitet gibt 1/[cos²(x)], sprich Eins-durch Kosinus-quadrat-x => Ableitungsregeln
… f(x) = tan(x) => Tangensfunktion
…(x) abgeleitet gibt 1/[cos²(x)], sprich Eins-durch Kosinus-quadrat-x
… gibt [cos(x)]^(-2), sprich: eins durch cosinus-quadrat-x => Ableitungen
