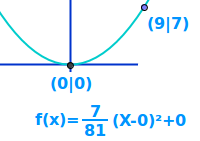
Scheitelpunktform aus zwei Punkten
Anleitung
Der Scheitelpunkt SP und anderer Punkt einer Parabelgleichung (quadratische Funktion) sind gegeben. Gesucht ist die Funktionsgleichung in Scheitelpunktform: f(x)=a(x-d)²+e => Ganzen Artikel lesen …
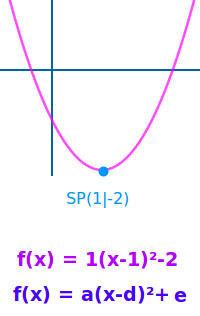Scheitelpunktform
f(x) = a·(x-d)² + e
Von quadratische Funktionen und Parabeln: aus der Scheitelpunktform y oder f(x) = a·(x²-d)²+e kann man leicht den Scheitelpunkt, die Öffnung und den y-Achsenabschnitt ablesen einer Parabel in einem xy-Koordinatensystem ablesen. Umgekehrt kann man sie leicht aufstellen, wenn man von einer Parabel den Scheitelpunkt SP und irgendeinen weiteren Punkt kennt. Das ist im Folgenden beschrieben. => Ganzen Artikel lesen …
Zwei
Als Zahl
Die Zwei ist die nächst natürliche Zahl nach der Eins. Das Zweifache nennt man auch das Doppelte. Als Hochzahl spricht man die Zwei auch als Quadrat aus: 3² ist 3 hoch 2 oder 3 quadrat. Hier stehen einige Besonderheiten zur Zahl Zwei. => Ganzen Artikel lesen …
f(x) oder y = a(x-d)² + e aus drei Punkten erstellen
Durch drei gegebene Punkte kann man oft (nicht immer) eine Parabel legen. Zu dieser Parabel kann man dann eine Funktionsgleichung anlegen. Wenn einer der drei Punkte bekanntermaßen der Scheitelpunkt der Parabel ist, dann lässt sich die Funktionsgleichung leicht über die Scheitelpunktform aufstellen. Dabei kann man zwei leicht unterschiedliche Methoden unterscheiden: => Ganzen Artikel lesen …
… Erklärung mit Aufgaben => Scheitelpunktform aus zwei Punkten
… Erklärung mit Aufgaben => Scheitelpunktform aus drei Punkten
… Erklärung mit Aufgaben => Scheitelpunktform aus zwei Punkten
… Erklärung mit Aufgaben => Scheitelpunktform aus zwei Punkten
… Erklärung mit Aufgaben => Scheitelpunktform aus zwei Punkten
