 Scheitelpunkte von Parabeln
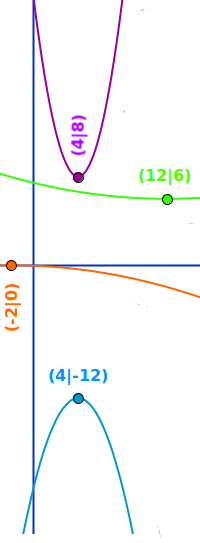
Scheitelpunkte von Parabeln
Beispiele
Der höchste und der tiefste Punkt einer Parabel heißt Scheitelpunkt. Man kann ihn aus einem Graphen ablesen, über die quadratische Ergänzung bestimmen oder auch mit Hilfe der ersten Ableitung f'(x). Hier stehen einige Beispiele von quadratischen Funktionen mit ihre Scheitelpunkten. => Ganzen Artikel lesen …
… von Parabeln, siehe unter => Scheitelpunkte von Parabeln
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
 Parabeln
Parabeln
Übersicht
Parabeln können Graphen sein, aber auch Flugbahnen oder Formen von Brücken, Spiegeln oder anderen Dingen. Das ist hier in einer Übersicht dargestellt. => Ganzen Artikel lesen …
 Schnittpunkte von Parabeln
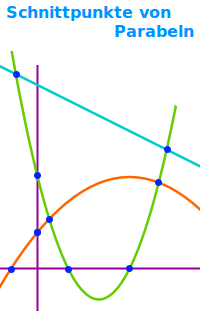
Schnittpunkte von Parabeln
Mit Koordinatenachsen, Geraden, Koordinatenachsen, Parabel
Eine Parabel meint hier den Graphen eine quadratischen Funktion. Diese Parabeln können Schnittpunkte mit verschiedenen anderen geometrischen Objekten haben. Hier werden ieinige kurz vorgestellt. => Ganzen Artikel lesen …
 Scheitelpunkt einer Parabel
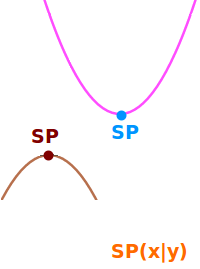
Scheitelpunkt einer Parabel
Höchster oder tiefster Punkt
Eine Parabel meint hier den Graphen einer quadratischen Funktion. Der Scheitelpunkt ist dann immer der höchste oder tiefste Punkt dieser Parabel, also entweder der Hoch- oder Tiefpunkt der Parabel. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Übersicht
Geraden können Schnittpunkte haben mit anderen Geraden, Koordinatenachsen, mit Ebenen oder Körpern. Man kann sie betrachten in einem 2D-Koordinatensystem (xy) oder in einem 3D-Koordinatensystem (xyz). Hier folgt eine knappe Übersicht. => Ganzen Artikel lesen …
… alle Verfahren unter => Scheitelpunkt einer Parabel bestimmen
… alle Verfahren unter => Scheitelpunkt einer Parabel bestimmen

