Rotationskörpervolumen berechnen
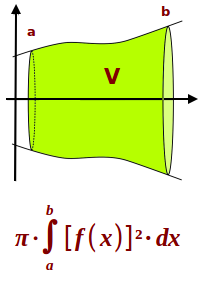
V = π·∫[f(x)]²·dx
Lässt man die Kurve (Graphen) einer Funktion f(x) einmal um die x-Achse kreisen (rotieren), dann entsteht durch diese Bewegung die Hülle eines Körper. Das Volumen des Körper kann mit Hilfe der Funktionsgleichung f(x) berechnet werden. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
Volumen über Integralrechnung
Der Graph einer Funktion f(x) wird um eine der Koordinatenachsen bewegt. Dadurch enstehen Körper wie etwa Zylinder, Kegel oder vasenartige Formen. Ihr Volumen kann mit Hilfe der Integralrechnung oft recht einfach bestimmt werden. Lies mehr unter => Rotationskörpervolumen berechnen
Formeln | Methoden
Volumen bezieht sich immer auf Körper, also 3D-Figuren. Ihr Volumen zu berechnen heißt, einen Zahlenwert zu finden, der ihren Rauminhalt in zum Beispiel Kubikzentimeter (cm³) oder Kubikmeter (m³) angibt. Eine Methodenübersicht dazu steht auf => Volumen berechnen
… pi mal r² mal h, mehr unter => Zylindervolumen
… siehe unter => Torusvolumen
