ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
1: Rabe

Ein großer schwarzer Vogel

Raben sind eng verwandt mit den etwas kleineren Krähen. Raben können bis zu 70 cm Körperlänge und ein Gewicht von 1,5 Kg erreichen. => Ganzen Artikel lesen …
2: Habe

Mathematisch

Als Substantiv ist die Habe das was jemandem gehört, also das Eigentum. Als Verb im Imperativ (Befehlsform) heißt es in der Mathematik so viel wie: nimm an dass. Dazu hier ein kurzes Beispiel. => Ganzen Artikel lesen …
3: Raben

… große schwarze Vögel, siehe unter => Rabe
4: Rate

Pro Zeit

Steigrate in Meter pro Sekunde bei Flugzeugen, Sterberate in Tote pro Tag oder eine Zinsrate in Euro pro Jahr: eine Rate ist immer eine Angabe mit einem Zeitbezug. In der Mathematik verallgemeinert man die Raten oft zur Änderungsrate. Ein Anteil der sich nur auf einen Zeitpunkt bezieht nennt man eine Quote. Für Beispiele siehe auch => Raten
5: Rauben

Bergbau

Als Rauben bezeichnet man im Bergbau die Entfernung von nicht mehr benötigen Ausbauelementen unter Tage, insbesondere des Ausbaus. Ein Motiv war es, wertvolle Rohstoffe (Stahl) wiederverwerten zu können. Ein anderer Anlass war der Wunsch, den Ausbau an anderer Stelle erneut verwenden zu können [1]. Die organisatorische Einheit zur Durchführung des Rauben war das Raubrevier. Den Rückbau größerer Anlagen nannte man => abrüsten
6: Krabbe

… das Schalentier, siehe unter => Nordseekrabbe
7: A-normale Parabel

… z. b. eine kubische Parabel, siehe unter => keine normale Parabel
8: ABC-Formel für Nullstellen von Parabeln

… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
9: ABC-Formel für Parabelnullstellenberechnung

… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel

f(x) = Ax² + Bx + C hat die Nullstellen [-B ± Wurzel aus (B² - 4A·C)] durch [2A]
10: ABC-Formel Parabel

… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
11: ABC-Formel und Parabelgleichung

… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
12: ABC-Parabelformel

x = [-b ± Wurzel aus (bb - 4ac)] durch [2a]

Neben der pq-Formel ist die sogenannte ABC-Formel die zweite Standard-Lösungsmethode für quadratische Gleichungen. Bei ihr darf vor dem x² eine beliebige Zahl als Faktor stehen. Das ist der Vorteil der ABC-Formel. Sie gilt für Gleichunen der Form: 0 = Ax²+Bx+C. Lies mehr unter => ABC-Formel
13: ABC-Parabelnullstellen

… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel

ABC steht für die sogenannte ABC-Formel zum Lösen quadratischer Gleichungen. Die Funktion f(x) = Ax² + Bx + C hat die Nullstellen [-B ± Wurzel aus (B² - 4A·C)] durch [2A]
14: Abnormale Parabel

… z. b. eine kubische Parabel, siehe unter => keine normale Parabel
15: Achsensymmetrische Parabel Nullstelle

Beispiel: f(x)=4x²+3 hat den Nullpunkt (0|3)

Eine achsensymmetrische Parabel hat eine reinquadratische Funktionsgleichung. Die Nullstelle liegt immer auf der y-Achse und bei x=0. Lies mehr dazu unter => Nullstellen von reinquadratischen Funktionen
16: Ähnlich Parabel aber quer

… siehe unter => gekippte Parabel
17: Ähnlich wie Parabel aber quer

… siehe unter => gekippte Parabel
18: Allgemeine Form der Parabelgleichung

y = Ax + Bx + C

A darf irgendeine Zahl außer der 0 sein, B und C sind vollkommen beliebig (dürfen auch 0 sein). Lies mehr unter => Allgemeine Form der quadratischen Funktion
19: Atypische Parabel

… z. b. eine kubische Parabel, siehe unter => keine normale Parabel
20: Atypische Parabeln

… z. b. eine kubische Parabel, siehe unter => keine normale Parabel
21: Aufgebogene Parabel

Gestaucht

Parabel meint hier: der Graph einer quadratischen Funktion. Als aufgebogen bezeichnet man eine Parabel, deren Äste gedanklich nach links und rechts gezogen (gebogen) wurden. Dadurch siehe die Parabel flacher und breiter aus. Der übliche Begriff dafür ist => gestauchte Parabel
22: Ausklammermethode für Parabelnullstellen

… siehe unter => Nullstellen von quadratischen Funktionen über Faktorisieren
23: Backenzahn-Parabel

… z. B. von einer biquadratischen Funktion, mehr unter => Backenzahnkurve
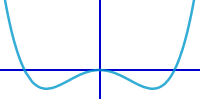24: Biquadratische Parabel

… der Graph von => biquadratische Funktion
25: Brennpunkt einer Parabel

… wo sich alle Strahlen treffen, siehe unter => Parabelbrennpunkt
26: Bronstein integrabel

… scherzhafter Ausdruck, mehr unter => Bronstein integrierbar
27: Dicke Parabel

… meint am ehesten eine => gestauchte Parabel
28: Dünne Parabel

… eine dünne und steile Parabel heißt => Gestreckte Parabel
29: einfache Parabel

… Graph von f(x)=Siehe unter => Normalparabel
30: einfachste Parabel

… Graph von f(x)=Siehe unter => Normalparabel
31: Elementare Parabel

… Graph von f(x)=Siehe unter => Normalparabel
32: Erstelle Parabelgleichung

… Übersicht unter => Parabelgleichung aufstellen
33: Erweiterte Normalparabel

kann mehrere Dinge bedeuten

- => Verschobene Normalparabel
34: Faktorisierte Form der Parabelgleichung

Eine quadratische Funktionsgleichung für eine Parabel

Zeichnet man für eine quadratische Funktion einen Graphen, so entsteht immer eine Parabel. Zu jeder Parabel kann man eine quadratische Funktionsgleichung aufstellen, die genau diese Parabel beschreibt. => Ganzen Artikel lesen …
35: Faktorisierungsmethode für Parabelnullstellen

… siehe unter => Nullstellen von quadratischen Funktionen über Faktorisieren
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023