Pyramidenhöhe
Geometrie
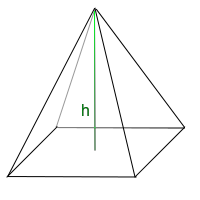
Strecke von der Spitze bis zum Fußpunkt: bei einer Pyramide stellt man sich gedanklich vor, dass man von der Spitze einen Stein senkrecht nach unten fallen lässt. Das Innere der Pyramide stellt man sich dazu hohl vor. Die Strecke, die der Stein (von der Spitze bis zum Fußpunkt) fallen würde ist die Höhe der Pyramide. Siehe auch => Pyramidenhöhenformel
Pyramidendach
Definition
Als Pyramidendach bezeichnet man ein Dach mit genau einer Spitzeund nur dreiecken Dachschrägen. Das Pyramidendach ist ein Sonderfall von einem => Zeltdach
Begriffsklärung
In der Geometrie unterscheidet man bei Pyramiden die Grundfläche, verschiedene Seitenflächen, eine Mantelfläche sowie die Oberfläche (Gesamtfläche). => Ganzen Artikel lesen …
… quadratisch, dreieckig, fünfeckig, mehr unter => Pyramiden
… Erklärung mit Berechnungstipp unter => Pyramidenmasse
Pyramidenhöhenformel
Berechnung
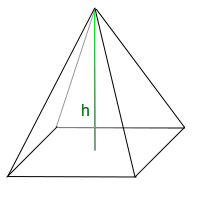
Sind das Volumen und die Grundfläche einer Pyramide bekannt, kann man daraus direkt die Höhe h berechnen. Die entsprechende Formel sowie auch Alternativen dazu sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Übersicht
Von der Spitze der Pyramide senkrecht bis auf den Boden: diese Strecke nennt man die Höhe h einer Pyramide. Zur Berechnung ihrer Länge gibt es verschiedene Ansätze. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Pyramidenhöhe über Pythagoras
Rechenwege
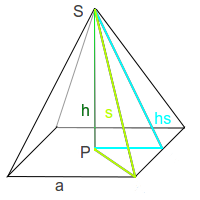
Die Höhe einer Pyramide ist die Strecke von der Spitze senkrecht herunter bis auf die Mitte der Grundfläche (Fußpunkt). Hier stehen zwei Varianten zur Berechnung der Länge der Pyramidenhöhe mit Hilfe des Satzes des Pythagoras. => Ganzen Artikel lesen …
Lösungsidee
Die Höhe h einer Pyramide ist die Strecke senkrecht von der Spitze bis zur Grundfläche. Kennt man die Länge der Pyramidenseitenkante und die Seitenlänge der Grundfläche, kann man daraus die Höhe h berechnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Lösungsidee
Die Höhe h einer Pyramide ist die Strecke senkrecht von der Spitze bis zur Grundfläche. Kennt man die Koordinanten der Eckpunkte der Grundfläche sowie die Koordinaten der Spitze, lässt sich daraus leicht die Höhe berechnen. => Ganzen Artikel lesen …
