Punktsymmetrie von Graphen
Übersicht
Wie für irgendeine Figur aus der Geometrie gilt auch für Graphen von Funktionen: wenn der Graph irgendeinen Symmetriepunkt hat, dann nennt man ihn punktsymmetrisch. Wenn dieser Symmetriepunkt der Ursprung (0|0) des Koordinatensystems ist, dann ist die entsprechende Funktion zusätzlich auch eine gerade Funktion. Das ist hier näher erklärt. => Ganzen Artikel lesen …
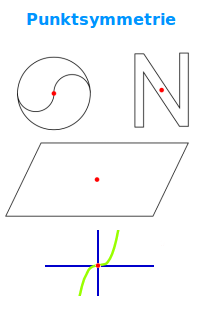Punktsymmetrie
Geometrie | Funktionsgraphen
Von Punktsymmetrie spricht man, wenn eine Figur (Geometrie, Graph) an einem Punkt gespiegelt werden kann und die Figur nach der Spiegelung wieder genauso aussieht wie vor der Spiegelung. In der Fachsprache heißt das, dass die Figur auf sich selbst abgebildet wird. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
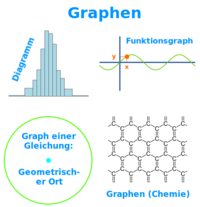Graphen
Arten
Funktionsraphen, Lösungsmengen von Gleichungen, Diagramme in der Statistik oder das Graphen (Betonung auf dem e) in der Chemie: hier stehen verschiedene Bedeutungen zu Graphen. => Ganzen Artikel lesen …
… am Punkt (0|0) gespiegelt, mehr unter => Punktsymmetrie von Graphen
Siehe auch
=> Punktsymmetrie von Graphen
Beispielliste
Punktsymmetrie von Graphen heißt in der Schulmathematik meist, punktsymmetrisch zum Koordinatenursprung, also zum Punkt (0,0). Ein Funktionsgraph ist genau dann punktsymmetrisch, wenn man ihn um 180° um den Punkt (0|0) drehen kann und er dann wieder genauso aussieht wie vorher. Mehr dazu unter => Punktsymmetrie von Graphen
… wie f(x)=Siehe unter => Punktsymmetrie von Graphen
Punktsymmetrie von Graphen überprüfen
Bedeutung | Methoden
Graphisch und rechnerisch: hier werden Methoden vorgestellt, wie man für eine gegeben Funktionsgleichung überprüft, ob der Graph punktsymmetrisch zu (0|0) ist. => Ganzen Artikel lesen …
